SOLUTION: Beginning at the origin, a spiral is constructed from 3 semi circles with centres at (1,0),(0,0),(2,0). The area of the shaded region, in u^2 is: A) 7 π-2 √3/6 B) 8 π-√3/

Algebra ->  Surface-area -> SOLUTION: Beginning at the origin, a spiral is constructed from 3 semi circles with centres at (1,0),(0,0),(2,0). The area of the shaded region, in u^2 is: A) 7 π-2 √3/6 B) 8 π-√3/      Log On


   

Question 1167553: Beginning at the origin, a spiral is constructed from 3 semi circles with centres at (1,0),(0,0),(2,0). The area of the shaded region, in u^2 is:
A) 7 π-2 √3/6
B) 8 π-√3/3
C)8 π-6 √3/3
D) 3 π -2 √3
E) 11 π -6√3/3

https://imageshack.com/i/pmBbsOMDj
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Call the origin O. Let A(2,0) be the center of the third semicircle, and let B(0,b) be the y-intercept of that third semicircle.

Triangle AOB is a 30-60-90 right triangle, because OA=2 and AB=4. That makes OB 2%2Asqrt%283%29.

The shaded region is (a) one-half the area of the second semicircle with radius 2, plus (b) one-third the area of the third semicircle (because angle BAO is 60 degrees), minus (c) the area of triangle AOB.

(a) %281%2F2%29%28pi%282%5E2%29%2F2%29+=+pi
(b) %281%2F3%29%28pi%284%5E2%29%2F2%29+=+%288%2F3%29pi
(c) %281%2F2%29%282sqrt%283%29%29%282%29+=+2sqrt%283%29

ANSWER: pi%2B%288%2F3%29pi-2sqrt%283%29+=+%2811%2F3%29pi-2sqrt%283%29

Note answer choices A, B, C, and E are all shown incorrectly, because required parentheses are missing.

Answer choice E is supposed to be the right answer: 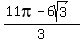%2811pi-6sqrt%283%29%29%2F3

But answer choice E as shown, 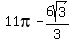11pi-6sqrt%283%29%2F3, is incorrect.