Question 1161726: A component (circle-shaped with a diameter measuring 60 cm) is stamped out of sheet steel. A square(with side measuring 30 cm) in the center of that circle is discarded. These components are stamped out of a continuous steel coil with a width of 70 cm. The stamping process requires a gap of 25mm between each component. The steel coil is supplied in lengths of 25 meters costing $200.
a) What is the approximate percentage of steel wasted including the center square?
b) Assuming minimal wastage, how many components can be produced from each 25-meter coil?
c) What is the approximate cost of a component if the scrap is sold at 50% of the cost?
Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! b) You can stamp up to  circles, circles,
Stamping the 60cm diameter circles centered on the mid-width of the sheet, 25mm (2.5cm) apart from each other would allow us to stamp along the 25m (2500cm) steel coil
 circles. circles.
In fact  circles with circles with  gaps between them, adding gaps between them, adding 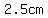 per gaps adds to a length of per gaps adds to a length of

and we could use the  leftover length leftover length
to leave some space between the circles at the ends and the beginning and end of the coil.
Offsetting the circles so they are shifted a bit to the left and the right, makes the string of circles a little shorter, but not short enough to fit an additional circle.
The most you could offset centers is  , ,
and making the distance between the centers centers  , would make the circles look like this , would make the circles look like this
 with with  and and   . .
Each pattern with 2 circles (red rectangle) takes up
 , so , so  circles require circles require  out of the out of the 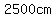 length of the coil. length of the coil.
a) The area of each circle is  
The area of the square cut off is  . .
The area of each component stamped is
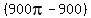   
The total area of the  stamped components is stamped components is

The area of a sheet coil 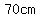 wide and wide and 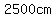 long is long is
 . .
Out of that surface area 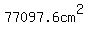 turns into turns into  components, and the rest is "steel wasted including the center square". components, and the rest is "steel wasted including the center square".
The surface area of the steel wasted including the center square" is

As a percentage of the 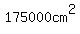 in the coil, that is in the coil, that is
  
c) The  of the coil wasted represents a cost of of the coil wasted represents a cost of  . .
Selling it at  of the cost reclaims of the cost reclaims  , ,
making the cost of  components components 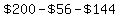 , and the cost per component , and the cost per component

|
|
|