SOLUTION: The sides of triangle XYZ are XY = XZ = 25 and YZ = 40. A semicircle is inscribed in triangle XYZ so that its diameter lies on YZ, and is tangent to the other two sides. Find the a

You are given the isosceles triangle XYZ.


Draw the perpendicular (the height, the altitude) from the vertex X to the base YZ.

Let A be the foot of this altitude.


According to the WELL KNOWN property of isosceles triangles, the altitude XA is the median at the same time.


Thus the original triangle XYZ is divided in two congruent right angled triangles XYA and XZA.

Their legs YA and ZA are 40/2 = 20 units long (each).


So, each of these two right angled triangles is (3,4,5) triangles with the hypotenuse of 25 inits long and 

with the legs of 20 units long (YA and ZA)  and 15 units long (the altitude XA).


The area of each of the two right angled triangles is 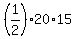  = 150 square units.


Now I will calculate the area of the triangle XYA by another way.


Draw the altitude in the triangle XYA from its vertex A to its hypotenuse XY.

Notice that this altitude's length is equal to the radius of the inscribed semi-circle (!)


  +---------------------------------------------+
  |                                             |
  |  It is the major point of the solution (!)  |
  |                                             |
  +---------------------------------------------+


So, if "r" be the radius of the seni-circle, then for the area of the triangle XYA we have this equation


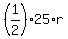     = 150,    or

     25*r     = 300.


Hence,  r = 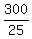 = 12 units.


So, the problem is just solved, and the  ANSWER  is  12 units for the radius and  

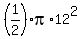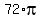 =  square units for the area of the semi-circle.