Question 1151099: In the diagram below, point X is the intersection of the two diagonals TW and UV of the cubical box illustrated. The shortest distance from point T to point Z is 4 sqrt3 cm. Find the area in cm2, of triangle XYZ.
Sry bout the other one.
Diagram: https://imgur.com/a/ciK5pIK
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! point  is the intersection of the two diagonals is the intersection of the two diagonals  and and 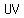 of the cubical box illustrated. of the cubical box illustrated.
The shortest distance from point  to point to point  is is 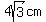 . and it is . and it is
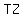 = solid diagonal = solid diagonal
Again, by the Pythagorean theorem we know that

 ........since cube, all sides are equal, so ........since cube, all sides are equal, so  and and 




 ........since cube, ........since cube, 
point  is the intersection of the two diagonals, is the intersection of the two diagonals,
triangle is isosceles, and altitude from  to to 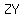 will bisect will bisect , let say at point , let say at point  and and  divides triangle divides triangle  into two right triangles into two right triangles
altitude from 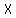 to to 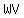 will bisect will bisect 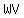 , let say at point , let say at point  , and the length of , and the length of 
now, connect points  and and  and you got right triangle and you got right triangle  whose side whose side  is altitude from is altitude from  to to 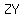
sides of this right triangle are:


find altitude  : :






then, the area of triangle  will be: will be:




|
|
|