.
Let x be the length of the side of the base, and
let y be the height of the container.
Then the volume is 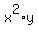 = 18000 cubic inches.
The cost of the material for two bases is
= 18000 cubic inches.
The cost of the material for two bases is 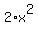 dollars;
the cost of the material for four lateral sides is 4*3*x*y = 12xy dollars.
The problem requires us to minimize
dollars;
the cost of the material for four lateral sides is 4*3*x*y = 12xy dollars.
The problem requires us to minimize  = 18000.
Using the restriction formula, express y =
= 18000.
Using the restriction formula, express y = 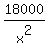 and substitute it into the total cost expression.
Then the cost takes the form C(x) =
and substitute it into the total cost expression.
Then the cost takes the form C(x) = 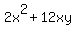 =
= 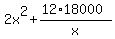 .
Thus the problem is just reduced to finding minimum of the function
C(x) =
.
Thus the problem is just reduced to finding minimum of the function
C(x) = 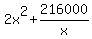 .
To find it minimum, take a derivative and equate it to zero. It gives you the equation
C'(x) =
.
To find it minimum, take a derivative and equate it to zero. It gives you the equation
C'(x) = 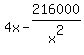 = 0,
which implies
4x^3 = 216000,
x^3 = 54000
x =
= 0,
which implies
4x^3 = 216000,
x^3 = 54000
x =  =
= 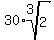 .
Then y =
.
Then y = 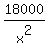 =
= 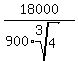 =
= 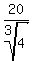 .
ANSWER. x=
.
ANSWER. x= 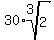 = 37.798 inches (approximately) and y=
= 37.798 inches (approximately) and y= 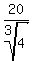 = 12.6 inches (approximately).
PARTIAL CHECK.
= 12.6 inches (approximately).
PARTIAL CHECK. 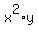 =
= 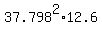 = 18001 in^3. The miserable difference is due to rounding.
= 18001 in^3. The miserable difference is due to rounding.
Solved.