SOLUTION: 16 inches are a combined perimeter of a circle and a square. What are the dimensions of the circle and square that produce a minimum total area?

Algebra ->  Surface-area -> SOLUTION: 16 inches are a combined perimeter of a circle and a square. What are the dimensions of the circle and square that produce a minimum total area?      Log On


   

Question 1148232: 16 inches are a combined perimeter of a circle and a square. What are the dimensions of the circle and square that produce a minimum total area?
Answer by ikleyn(52782) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let "x" be the square side length, and "y" be the radius of the circle.

Then

    4x + 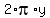2%2Api%2Ay = 16 inches                               (1)  (perimeter)

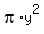    f(x,y) = x^2 + pi%2Ay%5E2   is the function to minimize   (2)  (area)


In other words, you should minimize (2) under the constraint (1).


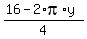From (1), express x = %2816-2%2Api%2Ay%29%2F4 = 4+-+0.5%2Api%2Ay  and substitute it into the function (2).

You will find then the function to minimize in the form

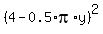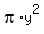    g(y) = %284-0.5%2Api%2Ay%29%5E2 + pi%2Ay%5E2 = 

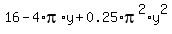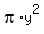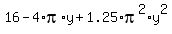         = 16+-+4%2Api%2Ay+%2B+0.25%2Api%5E2%2Ay%5E2 + pi%2Ay%5E2 = 16+-+4%2Api%2Ay+%2B+1.25%2Api%5E2%2Ay%5E2.


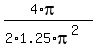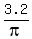This quadratic function of "y" has the minimum at  y = " -b%2F%282a%29 " = %284%2Api%29%2F%282%2A1.25%2Api%5E2%29 = 3.2%2Fpi.    


ANSWER.  The values that provide the minimum of the total area are

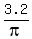         y= 3.2%2Fpi inches (the circle radius)  and  

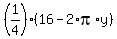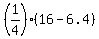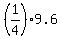         x = %281%2F4%29%2A%2816+-+2%2Api%2Ay%29 = %281%2F4%29%2A%2816+-+2%2Api%2A%283.2%2Fpi%29%29 = %281%2F4%29%2A%2816-6.4%29 = %281%2F4%29%2A9.6%29 = 2.4 inches (the side of the square).

Solved.