SOLUTION: A dog owner wants to enclose a rectangular area and has $840 to spend on fencing. She wants the side of the lot facing the road to have a fancier fencing material costing $18 per f

Let x be the length of the side facing the road.

and let y be the length of the adjacent side.


Then the cost of the fence is 18x + 6x + 6y + 6y = 24x + 12y.

Thus we need to maximize the area  xy  under the condition  24x + 12y = 840.


Or, which is EQUIVALENT, to maximize xy under the condition 2x + y = 70.


Express y = 70 -2x from the condition. Then we need maximize this quadratic function

f(x) = x*(70-2x) = -2x^2 + 70x.


The roots of this quadratic function are x= 0  and x= 35,  so the maximum of the quadratic function is achieved 

    at the midpoint between the roots  x= 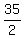 = 17.5.


Answer.  The facing to the road side must be 17.5 ft long.

         The adjacent side must be  y= 70-2x = 70 - 2*17.5 = 35 ft long.


         Then the area is 17.5*35 square ft  and the cost (Check !)  = 18*17.5 + 6*17.5 + 35*6 + 35*6 = 840 dollars.   ! Correct !