SOLUTION: So I have this dodecagon with the side length of 2, it is inscribed in a square. How do i find the area of the square with only that information?

Algebra ->  Surface-area -> SOLUTION: So I have this dodecagon with the side length of 2, it is inscribed in a square. How do i find the area of the square with only that information?      Log On


   

Question 1113612: So I have this dodecagon with the side length of 2, it is inscribed in a square. How do i find the area of the square with only that information?
Found 3 solutions by stanbon, greenestamps, ikleyn:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
So I have this dodecagon with the side length of 2, it is inscribed in a square. How do i find the area of the square with only that information?
-----
Sketch the square
Draw a line segment connecting the midpoints of the sides.
Note: That line has length equal to the side of the square.
Call it "the center line".
-----------------------------------------------------------
Sketch half of the dodecagon in the top half of the square
Connect each of the six vertices to the center of the square
--------------
Note:: 360/12 = 30 degrees
Note: You have 6 triangles in the top half of the square
Note: The base of each of the triangles has length 2
Note: Using the triangle on "the center line::
Draw a perpendicular bisector of its base.
That forms a right triangle with base = 1, central angle = 15 degrees,
and hypotenuse = (1/2) the side of the square = "r"
---
Then sin(15 deg) = 1/r
r = 1/sin(15) = 3.864
Then side of square = 2*3.864 = 7.727
Ans : Area of the square = 59.71 sq.units
-----------
Cheers,
Stan H.
-----------------
--

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Obviously you mean a regular dodecagon; otherwise the problem can't be solved....

Let A, B, C, D, and E be consecutive vertices of the dodecagon; with sides AB and DE on adjacent sides of the square.

Let F be the corner of the square determined by the extension of sides AB and DE of the dodecagon; that is, AF and FE are portions of adjacent sides of the square.

Draw segments from vertex C of the dodecagon parallel to AF and FE, forming a small square in the corner of the big square. The area outside the dodecagon and inside the square now consists of that small square and two small right triangles.

The exterior angle of a regular dodecagon is 30 degrees; that means the small right triangles are 30-60-90 right triangles. The hypotenuse of each of those triangles is a side of the dodecagon, with length 2. Then the lengths of the legs of the triangles are 1 and sqrt(3).

Then by symmetry the full side length of the large square is
1%2Bsqrt%283%29%2B2%2Bsqrt%283%29%2B1+=+4%2B2%2Asqrt%283%29

Then the area of the square is %284%2B2%2Asqrt%283%29%29%5E2+=+28%2B16%2Asqrt%283%29

----------------------------------------------------------


Alternate solution method....

Trigonometry makes this easy.

Let AB be a side of the dodecagon which lies on a side of the square, and consider the triangle OAB where O is the center of the figure (center of both the square and the dodecagon).

If M is the midpoint of AB, then OM is an apothem of the dodecagon; and the length of the apothem is half the side of the square.

Angle AOB is 30 degrees, so angle AOM is 15 degrees.

With AB being 2, AM is 1, so the length of the apothem is 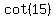cot%2815%29.

Then the side length of the square is 2%2Acot%2815%29+=+2%282%2Bsqrt%283%29%29+=+4%2B2%2Asqrt%283%29, as before.

Answer by ikleyn(52785) About Me  (Show Source):
You can put this solution on YOUR website!
.
Go to Wikipedia and look in this its article https://en.wikipedia.org/wiki/Dodecagon 

talking about dodecagon (it is better one time to see than 100 times to hear).


Dodecagon has 12 sides. We consider a REGULAR dodecagon.


Look in the figure in this article.


In my solution, I consider the scheme when 4 vertices of the regular dodecagon coincide with the midpoints of square sides.


I will work with 3 sides of the regular dodecagon that are located in QIII.


These three sides are sloped at 15°, 45° and 75° to the horizontal line.


The sides are of 2 units long each.


It means that half of the square side length is this sum


a%2F2 = 2*cos(15°) + 2*cos(45°) + 2*cos(75°) = 2%2Acos%28pi%2F12%29+%2B+2%2Acos%28pi%2F4%29+%2B+2%2Acos%285pi%2F12%29 = 3.866.


Hence, the square side length = 2*3.866 = 7.731.


Then the square area = a%5E2 = 7.731%5E2 = 59.772.


Answer.  The square area = 59.772 square units (approximately).

Notice that in his solution @greneestamps considers different scheme of the regular dodecagon inscribed to the square.