SOLUTION: A close cylindrical tank 10ft in height and 4ft in diameter contains water with depth of 3ft and 5 inches. What would be the height of the water when the tank is lying in a horrizo

First, convert dimensions from feet to inches:  H = 10 ft = 120 in,  h = 3 feet 5 inches = 12*3+5 = 41 in,  r = 2 ft = 24 inches.

The volume of the tank is  V =  =  = .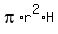

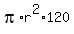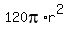The filled volume of the tank is  F =  = .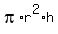

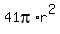The ratio of the filled part to the total volume is   = .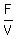

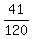In any position (vertical/horizontal) the filled part is 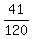  of the total volume.

Hence, we need to find the central angle of the circle which subtends the segment of the circle whose area is 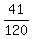 of the circle area.

The area of the segment of a circle is  A = 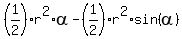,  where  is the central angle in radians.

Hence, we need to solve the equation

 = ,

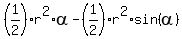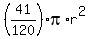or, canceling r^2 in both sides

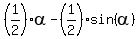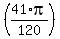 =  = 1.07283.


I solved this non-linear equation using Excel function  "Goal Seek" of  the section "What-if"  in my computer.

The answer is  = 2.633 radians.

Since the problem asks about the depth, it is 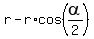  = 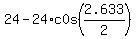 = 17.96 inches.     (24 = 24 inches = r = 2 ft is the radius)