Question 1078575: Find the total area of a cone with a height of 15 and a volume of 320pi
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The volume of a cone is volume = (1/3)(area of the base)(height),
so area of the base =3(volume)/height
The area of the base of this cone is
area of the base = . .
It would be good to know the radius,  , of that circular base. , of that circular base.
The area of a circle of radius  is is  , ,
so in this case  --> -->  --> -->  . .
At this point, you could look up a formula for the total area of a cone,
and apply it.
I looked up, and found
 , and , and

with r, s, and h being
the radius of the base, the slant height, and the cone height.

For those who want to understand rather than memorize formulas,
or use formulas without wondering why it is so:
The  term represents the area of the circular base. term represents the area of the circular base.
 comes from the Pythagorean theorem comes from the Pythagorean theorem
applied to a cross section of the cone going through its axis.
The 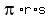 term represents the lateral area, term represents the lateral area,
and that is an expression you could figure out by yourself, either
1) by considering the lateral area to be
the area of a pyramid with infinity of lateral faces
and a base perimeter of 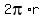 , or , or
2) by thinking that the lateral area, peeled of and flattened out
would be a sector of a circle of area 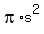
amounting to  of the entire circle). of the entire circle).
|
|
|