Question 1071413: Two concentric circles are shown. The radius of the inner circle is 3, and the distance between the circles is 3. A line segment of length 4 has its endpoints on both circles. Compute the distance from point A to point B.
Image in the link: http://prntscr.com/eg347w
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Assume that the center of the circles is the origin (0,0),
The outer circle is,
1.
If we make a circle centered at the intersection of the 3 and 4 lines with a radius of 4, it would be,
2.
We can find the intersection of the outer circle and the new circle,
From 1,
Substituting into 2,
So then,
So now find the distance between ( , ) and ( , ).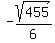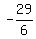
.
.
.
 .
|
|
|
