SOLUTION: I have Three Equal Inscribed Circles Into Big Circle. Diameter of internal circles is 5 mm. How I calculate area of outer circle.

     Three Equal Circles  are Inscribed Into Big Circle in a way they touch each other. 
     Diameter of internal circles is 5 mm. Calculate the area of outer circle.

Let the points A, B and C be the centers of the three small circles. 
Draw the segments AB, AC and BC. 
You will get an equilateral triangle ABC, obviously.

The sides of this triangle have the length twice the radius of the small circles, i.e. 10 mm. Obviously.

In other words, the side length of this equilateral triangle is a = D = 5 mm.

The length of any altitude of this equilateral triangle is  h = . (well known fact, actually) 

From the symmetry, it is clear that the intersection point of all three altitudes of the triangle ABC coincides with the center 
of the large circle O. 

Since the three altitudes of the triangle ABC coincide with its medians, the intersection point O divides each altitude/median
in proportion 2:1, counting from the vertex to the base.

Therefore, each of the three segments OA, OB and OC has the length  = .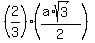

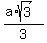Then the radius of the large circle is  R = |OA| +  = .

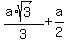Now you can calculate R on your own by substituting a = 5 mm into the last formula, and then calculate the area of the large circle A = .