Question 1070529: Let ABC be a triangle such that AB= 6cm, AC=8cm and BC 10cm and M be the midpoint
of BC .AMDE is a square, MD and intersects AC at point F . Find the area of quadrilateral AFDE.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Here is triangle ABC with midsegments LM and MN 
You know that those midsegments are parallel to
and half the length of the side they do not touch.
That makes ALMN a rectangle.
Line AM is the diagonal of rectangle ALMN.
Triangle ABC is a  times scaled-up version of the most popular 3-4-5 right triangle,
with side lengths in cm of
 ,
 , and
 .
It has a smaller acute angle ACB (opposite shorter side AB),
a larger acute angle ABC, and a right angle BAC (opposite longest side BC).
The mid segments, and AM split triangle ABC into four smaller triangles.
They are all 3-4-5 right triangles with sides measuring
 ,
 ,
 ,
congruent smaller acute angles (so that  for example),
and congruent larger acute angles, as well.
Since they tell us that "MD and intersects AC at point F",
I know to what side of segment AM square AMDE is locate,
and I can draw the square, like this
 
and triangle MFA is a right triangle,
similar to LMA and all the other 3-4-5 triangles we looked at before,
because it shares the same smaller acute angle CAM with triangle LMA.
So, for MFA, the shorter leg to longer leg ratio is the same
 -->  -->  -->  
 
|
|
|
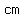
