SOLUTION: ΔABC has vertices at A(8,3), B(7,5), and C(2,4). Point D, located on AC¯ at approximately (6.7,3.22), is the intersection of the altitude drawn from B to AC¯. https://cds.f

Algebra ->  Surface-area -> SOLUTION: ΔABC has vertices at A(8,3), B(7,5), and C(2,4). Point D, located on AC¯ at approximately (6.7,3.22), is the intersection of the altitude drawn from B to AC¯. https://cds.f      Log On


   

Question 1064074: ΔABC has vertices at A(8,3), B(7,5), and C(2,4). Point D, located on AC¯ at approximately (6.7,3.22), is the intersection of the altitude drawn from B to AC¯.
https://cds.flipswitch.com/tools/asset/media/601653
The area of △ABC is _____ units2.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Segment BD is perpendicular to segment CA. What is the exact intersection point of lines BD and CA? How far is point D from point B?


line CA
y-3=%28%284-3%29%282-8%29%29%28x-8%29
y-3=-%281%2F6%29%28x-8%29
slope is -1%2F6.


line BD
Need slope to be 6.
y-5=6%28x-7%29


Now, again, what is the intersection of line CA and BD?
system%28y-3=-%281%2F6%29%28x-8%29%2Cy-5=6%28x-7%29%29
system%286y-18=-x%2B8%2Cy=6%28x-7%29%2B5%29
system%28x%2B6y=26%2Cy=6x-42%2B5%29
system%28x%2B6y=26%2Cy=6x-37%29
system%28x%2B6y=26%2C6x-y=37%29
-
x%2B6%286x-37%29=26
x%2B36x-6%2A37=26
37x=26%2B6%2A37
highlight%28x=248%2F37%29
-
y=6%28248%2F37%29-37
y=6%2A248%2F37-37%5E2%2F37
y=%286%2A248-37%5E2%29%2F37
highlight%28y=119%2F37%29
Point D is at system%28x=248%2F37%2Cy=119%2F37%29


What is the distance between D and B? This is the altitude for the base AC.

Area for the triangle, %281%2F2%29%2AAC%2ABD

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

ΔABC has vertices at A(8,3), B(7,5), and C(2,4). Point D, located on AC¯ at approximately (6.7,3.22), is the intersection of the altitude drawn from B to AC¯.
https://cds.flipswitch.com/tools/asset/media/601653
The area of △ABC is _____ units2.
Just calculate the length of AC, the base, using the distance formula: d+=+sqrt%28%28x%5B1%5D+-+x%5B2%5D%29%5E2+%2B+%28y%5B1%5D+-+y%5B2%5D%29%5E2%29, and the length of the altitude, or BD.

Now, take half the product of AC and BD, since the area of a triangle is calculated as 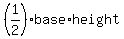%281%2F2%29+%2A+base+%2A+height

That's all.......nothing too COMPLEX and/or CONFUSING.