SOLUTION: Compute for the value of {{{int(int((1/(1+4x^2+9Y^2)^2), dx,-infinity, infinity),dy, -infinity, infinity)}}}

1.  Let me show first how to calculate more simple integral 


    .      (1)


    Change variables for polar coordinates x = 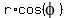,  y = .

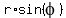    Then dx*dy = 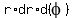, and the integral (1) becomes 

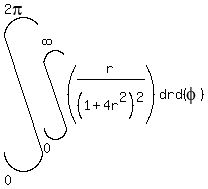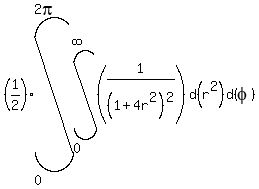     =  = (introduce new variable z = ) = .


    The internal integral is 
                                                          |
     =   =  |         =  .
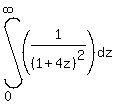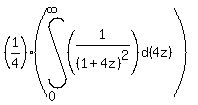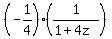                                                          |0

    Then the entire double integral (1) is   = .



2.  Now, let us start with the original integral  

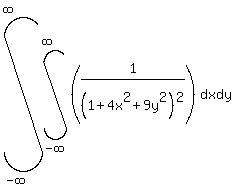    .      (2)

To calculate this integral, let me introduce the new coordinate system 

   u = x,
   v = .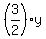

Then

   x = u,  y = 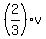;  dx = du, dy = 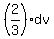, and the integral (2) becomes


   .

   The integral of "u" and "v" after the factor 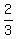 was just calculated in the section #1.

   Hence, the final answer is  = .