Question 1061895: The void cube is a 3 𠖧 cube with a hole through the centre of each face. If the side length of each small cube is 1 cm, what is the surface area in square cmon the void cube. Thanks
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The total of surface area (in square cm) on the void cube is  . .
ONE APPROACH:
Let us start with a large cube made of  smaller cubes of side length smaller cubes of side length  . .
After making the holes,
we end up with only the small cubes attached to the edges of the original large cube.
The large cube originally had (and ends up still having)  edges; edges;
 horizontal edges on the bottom base, horizontal edges on the bottom base,
 horizontal edges on the top base, horizontal edges on the top base,
and  vertical connecting edges. vertical connecting edges.
There were (and are)  vertices: vertices:
 on the bottom base, on the bottom base,
and  on the top base. on the top base.
On the void cube, each edge has
one central small cube, attached to  other cubes, with other cubes, with  faces exposed. faces exposed.
of the remaining small cubes on the edges, each one is on one of the  attached to attached to  other small cubes, leaving other small cubes, leaving  of its faces exposed. of its faces exposed.
There is a total of
 small cube face surfaces. small cube face surfaces.
ANOTHER APPROACH:
Before making the holes, we had a large solid cube with edge length = 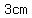 . .
 and and 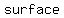  for the solid cube. for the solid cube.
We could start with a large solid cube made of  smaller smaller  cubes, cubes,
looking like a Rubik cube.
From the large solid cube,
we first tunnel top to bottom through the middle of the top face,
removing 3 small cubes,
including the 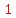 central core cube, central core cube,
which in a Rubik cube would have no colored faces.
Then, back on our large holey cube,
we tunnel front to back from the front face,
this time removing only  more small cubes, more small cubes,
because the 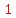 central core cube has been removed before. central core cube has been removed before.
Finally, we tunnel left to right from the left side through the large holey cube,
removing another  more small cubes. more small cubes.
We have removed  small cubes from the original large solid un-holey cube. small cubes from the original large solid un-holey cube.
If we put back together the small cubes removed,
the same way they were attached to each other before,
we have something familiar anyone who ever took apart a Rubik cube.
There is a central core cube,
completely covered on all  faces by faces by  other small cubes. other small cubes.
That is a total of 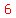 small cube face surfaces removed from the original large cube. small cube face surfaces removed from the original large cube.
Only  faces of those faces of those  small cubes are exposed small cubes are exposed
(the other one is attached to the central core cube).
Of those  exposed faces, exposed faces,
the  outermost face was the center of a face of the larger solid cube. outermost face was the center of a face of the larger solid cube.
(If we started with a Rubik cube,
those  outermost faces, outermost faces,
 face on each of face on each of  small cubes, are colored). small cubes, are colored).
The other  faces on each of those still exposed faces on each of those still exposed  removed small cubes, removed small cubes,
is a newly exposed surface.
That is a total of  newly exposed small cube face surfaces. newly exposed small cube face surfaces.
Meanwhile, on the original cube, while converting it into the holey void cube,
we have removed 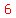 small cube face surfaces, small cube face surfaces,
and we have newly exposed  small cube face surfaces, small cube face surfaces,
for a total of  small cube face surfaces. small cube face surfaces.
|
|
|