Question 1048269: A right triangle has one vertex on the graph of y=x^5 , x>0, at (x,y) another at the origin, and a third on the positive y-axis at (0,y). Express the area A of the triangle as a function of x
Found 2 solutions by MathLover1, advanced_Learner:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! A right triangle has one vertex on the graph of  , ,  , at ( , at ( , , ) )
another at the origin, or ( , , ) )
and a third on the positive y-axis at ( , , ) )
remember, we let  ; so, replace " ; so, replace " " with " with 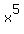 to get ( to get ( , ,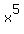 ) )
let's draw a picture:

since the point ( , , ) is " ) is " " units to the " units to the 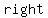 and " and " " units " units  , this means that the , this means that the 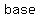 of the triangle is " of the triangle is " " units long and the " units long and the 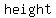 is " is " " units " units
So the base is " " and the height is " and the height is 
Now recall (or look up), the area of any triangle is
 ..........substitute ..........substitute  and and 


Answer by advanced_Learner(501)   (Show Source): (Show Source):
|
|
|