.
A  frustum of pyramid consists of square base of length 10 cm and a top square of 7 cm.
frustum of pyramid consists of square base of length 10 cm and a top square of 7 cm.
The heights of the  frustum is 6 cm calculate
frustum is 6 cm calculate
(A) the surface area
(B) volume
~~~~~~~~~~~~~~~~~~~~~~
Volume
See this Wikipedia article or this WEB-page.
The volume formula of a frustum of a square pyramid was introduced by the ancient Egyptian mathematics
in what is called the Moscow Mathematical Papyrus, written ca. 1850 BC.:
V = 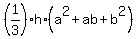 where a and b are the base and top side lengths of the truncated pyramid, and h is the height.
The Egyptians knew the correct formula for obtaining the volume of a truncated square pyramid,
but no proof of this equation is given in the Moscow papyrus.
where a and b are the base and top side lengths of the truncated pyramid, and h is the height.
The Egyptians knew the correct formula for obtaining the volume of a truncated square pyramid,
but no proof of this equation is given in the Moscow papyrus.
By applying the formula, we get V = 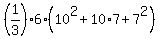 = 438
= 438  .
.
By the way, the proof is easy.
As you know, the volume of the larger pyramid is  =
= 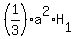 , where
, where 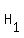 is its height.
The volume of the smaller pyramid is
is its height.
The volume of the smaller pyramid is  =
= 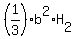 , where
, where 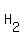 is its height.
Obviously, from similarity
is its height.
Obviously, from similarity 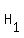 =
=  and
and 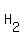 =
= 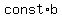 , where const is a constant value independent of "a" and "b".
Then
, where const is a constant value independent of "a" and "b".
Then  =
= 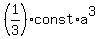 ,
,  =
= 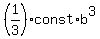 .
The volume of the frustum is the difference
V =
.
The volume of the frustum is the difference
V = 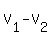 =
= 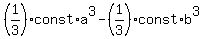 =
= 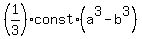 =
= 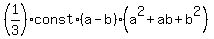 .
But const*(a-b) =
.
But const*(a-b) = 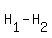 = h, the height of the frustum.
Therefore, the volume of the frustum is V =
= h, the height of the frustum.
Therefore, the volume of the frustum is V = 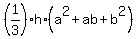 . QED.
. QED.