Question 1043104: Two perpendicular chords divide a circle with a radius of 13 cm into four parts. If the perpendicular distances of both chords are 5 cm each from the center of the circle, find the area of the smallest part.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two perpendicular chords divide a circle with a radius of 13 cm into four parts.
If the perpendicular distances of both chords are 5 cm each from the center of the circle,
find the area of the smallest part.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The Figure is on the right.
AB and CD are two given perpendicular chords.
Let the Point E be their intersection point.
We need to find the area of the shape EBC.
Draw the radius OF through the point E.
It is clear that this radius cuts the shape EBC in two congruent parts,
EBF and EFC, and each of them has the area half of the area EBC.
Also draw the radius OX (horizontal line) and the radius OC.
Let G is the intersection of OX and CD.
Then |OG] = 5, |OC| = 13, and the triangle OGC is a right-angled.
Then |GC| = 12 (Pythagorean triangle 5, 12, 13).
The angle COX = 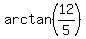 = 1.176 radians.
The angle FOX = 45° = = 1.176 radians.
The angle FOX = 45° =  radians. radians. |
 Figure.
Figure.
|
Then the angle COF = 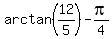 = = 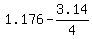 = 0.391 radians, and we can consider it as a known value.
Let us denote this angle COF as = 0.391 radians, and we can consider it as a known value.
Let us denote this angle COF as  : :  = 0.391 radians.
Now we are on the straight finish line.
The area of the sector COF is = 0.391 radians.
Now we are on the straight finish line.
The area of the sector COF is 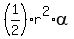 = 33.04 = 33.04  , and all we need to do is to distract the area of the triangle OEC.
The area of the triangle OEC is , and all we need to do is to distract the area of the triangle OEC.
The area of the triangle OEC is  .|EF|*|OG| = .|EF|*|OG| =  = 17.5 = 17.5  . (the segments EF and OG are the base and the altitude of the triangle)
Hence, the shape EFC has the area 33.04 - 17.5 = 15.54 . (the segments EF and OG are the base and the altitude of the triangle)
Hence, the shape EFC has the area 33.04 - 17.5 = 15.54  .
Then the shape EBC has the area twice of it: 2*15.54 = 37.08 .
Then the shape EBC has the area twice of it: 2*15.54 = 37.08  .
Answer. The shape EBC has the area of 37.08 .
Answer. The shape EBC has the area of 37.08  . .
|
|
|