SOLUTION: Find the straight lines which have slope -1 and form a triangle of area 8 square units with coordinate axes.

Since the slope is -1, we substitute -1 in the
slope intercept form

y = mx + b 

and get

y = -1x + b

or

y = -x + b


The y coordinate is (0,b).

We find the x-intercept by substituting y=0 and solving
for x:

0 = -x + b

x = b

So the x-intercept is (b,0)

We graph a typical such line:



We want the area of the green triangle:

The area of a triangle is given by the formula:



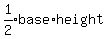The base is b and the height is also b
We are give that the area = 8, substituting:





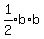
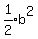Multiply through by 2



Take square roots of both sides, remembering ±





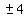
So there are two triangles. One for b=4 and one 
for b=-4, the two green triangles below:
 


Edwin