Question 1030360: Find the surface area
Shipping companies often use containers that are triangular solids to ship prints and other documents that are rolled so the cylinders would not roll around in the truck. What is the surface area of a triangular prism container that would be needed to enclose a rolled document with a diameter of 10cm and a length of 90cm? Round your answer to the nearest tenth. Assume the triangular face is an equaliateral triangle
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! for the following comments, refer to the first diagram shown here.
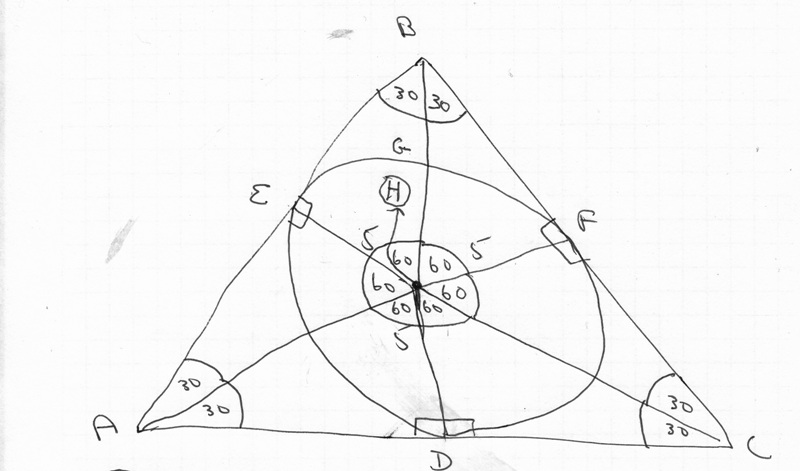
the center of the circle is H.
the circle is formed by EGFD
the radii of the circle perpendicular to the sides of the equilateral triangle are DH, EH, FH.
the equilateral triangle is ABC.
the height of the triangle is BD which is composed of line segments BH and HD.
the base of the triangle is AC which is composed of the line segments AD and DC.
the lines from the center of the circle to the corners of the equilateral triangle are AH, BH, and CH.
note that BH, which is part of the height of the triangle BD, is one of them.
the equilateral triangle ABC is divided into 3 equal isosceles triangles.
they are AHB, BHC, and AHC.
these triangle are congruent to each other.
their altitude are EH, FH, and DH, respectively.
the length of their altitudes is the length of the radius of the circle which is 5 cm (half the length of the diameter of the circle).
they are all 30,60,90 degree triangle.
we'll use one of those triangle for now.
that triangle will be AHC.
that triangle is composed of two right triangles.
they are AHD and CHD.
we can use trigonometry to solve for DC and to solve for HC.
DC is the base of triangle CHD, and HC is the hypotenuse of triangle CHD.
sine of angle DCH is equal to sine (30) is equal to HD / HC.
HD is equal to 5, so we get sine(30) = 5/HC.
solve for HC to get HC = 5 / sine(30) = 10 cm.
tangent of angle DCH is equal to HD / DC.
since angle DCH is 30 degrees and HD is 5 cm, you get tan(30) = 5 / DC.
solve for DC to get DC = 5 / tan(300 = 8.660254038.
we have:
HC = 10
DC = 8.660254038.
since AD is equal to DC, then AC is equal to 2 * DC = 17.32050808.
snce BH is equal to HC, we have:
BD is equal to BH + HD = 5 + 10 = 15.
we now have:
BD = 15
AC = 17.32050808.
BD is the height of triangle ABC.
AC is the base of triangle ABC.
the area of triangle ABC is equal to 1/2 * base * height which is equal to 1/2 * 17.32050808 * 15.
this makes the area of triangle ABC equal to 129.9038106 square cm.
that's the area of the base of your triangular prism.
for the following comments, refer to the second diagram shown here.
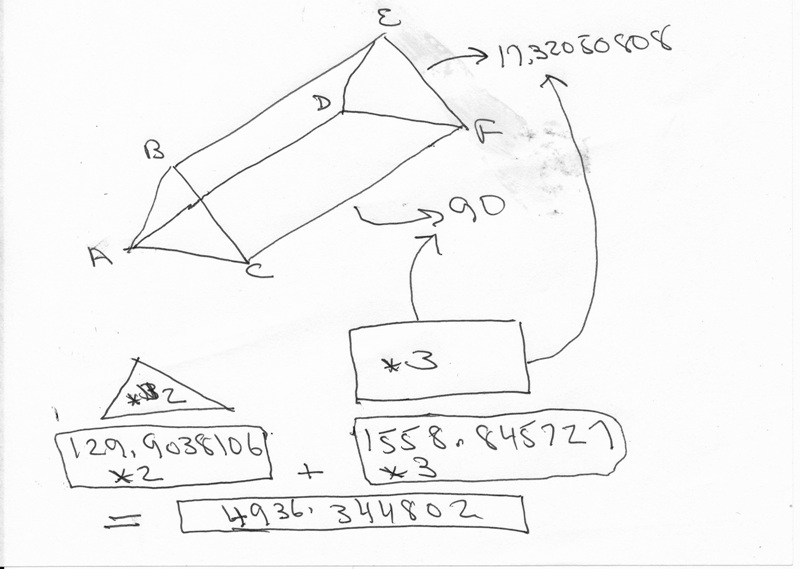
the triangular prism is ABCDEF.
the two bases are triangle ABC and triangle DEF.
these triangle are congruent and have the same area each of 129.9038106 square cm.
the three rectangles connecting the triangles have the height of the prism as one of their side lengths and the length of a side of the equilateral triangles as their side widths.
the three rectanghles are ABED, ACDF, BEFC.
the area of each of these rectangles is 90 * 17.32050808 = 1558.845727 square cm.
the surface area is equal to 2 times the area of the base plus 3 time the area of one of the sides.
that would be 2 * 129.9038106 + 3 * 1558.845727 = 4936.344802 square cm.
i confirmed with an online calculator that this is correct.
|
|
|