Question 1011941: Find the side of a regular octagon inscribed in a circle of radius 19 cm.
Found 2 solutions by It is costly, KMST:
Answer by It is costly(175)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Think TRIANGLES. Triangles are the key to solving many problems.
They are at the heart of geometry, trigonometry and engineering.
Or think TRIGONOMETRY, if you wish.
Use LAW OF COSINES, if that is what you were taught recently.
Here is the circle, with its center, the inscribed regular octagon,
and some line segments that are at the same time
diameters of the circle and diagonals of the octagon.

The diagonals connecting opposite octagon vertices go through the center of the circle,
and split the octagon into  isosceles triangles. isosceles triangles.
Each of those triangles has two sides measuring 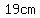
(the radius of the circle), and an angle measuring
 (or (or  if you prefer radians) if you prefer radians)
at the center of the circle.
USING TRIANGLES:
Let's look at one of those triangles, and use the Pythagorean theorem
  ---> ---> ---> ---> ---> ---> for the larger right triangle. for the larger right triangle.
For the smaller right triangle,  . .
We can substitute 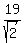 for for  (and (and 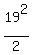 for for  if you wish) if you wish)
sooner or later, as you wish.
 <--> <--> <--> <--> <--> <-->



 ---> ---> ---> ---> or for an approximate measure or for an approximate measure  (rounded) (rounded)
USING TRIGONOMETRY:
We can put one of those triangles on a set of coordinates to find the distance between the vertices of the octagon.
Here are two similar triangles:
 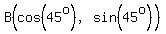 = =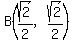 , and , and  , ,
so 
  is the length of the side of the octagon, in cm. is the length of the side of the octagon, in cm.
USING LAW OF COSINES:
 Law of cosine says that Law of cosine says that  , so with length measured in cm, , so with length measured in cm,




 , ,
and  is the length of the side of the octagon, in cm. is the length of the side of the octagon, in cm.
|
|
|