Question 1006486: a wire cross section diameter decresed 5% then volumes equal which percentage length increased
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the diameter decreases by 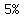 , ,
it becomes  of the original diameter. of the original diameter.
As a consequence, the cross-section surface area,
 , ,
becomes
 . .
It becomes  of the original cross-section surface area. of the original cross-section surface area.
As the wire can be considered a cylinder,
with a base the same size/shape as the circular cross-section,
and the length of the wire for a height,
the original wire's volume is
 . .
The new wire's volume is
 . .
Since that volume has to be the same,
 --> --> --> -->
The relative change in length is
   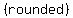 . .
We cannot give an exact decimal value,
we have to give a rounded, approximate result,
as 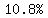 , or , or 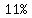 , for example, , for example,
because 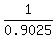 and and 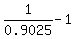 written as decimals would have an infinite number of digits. written as decimals would have an infinite number of digits.
Since we start with two significant figure in 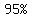 , ,
reporting the result as 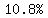 (very similar precision), (very similar precision),
or 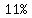 (same number of significant digits) makes sense. (same number of significant digits) makes sense.
NOTE:
If all that talk about precision and significant figures, doesn't make sense to you, pretend that I did not write that.
|
|
|