Question 935840: You play the following game with your worst enemy, who wishes to keep your score down. A
referee gets to pick a positive integer n. Then your enemy gets to pick n different real numbers.
You get to multiply different pairs of these numbers together, as many different pairs as you
want. You get one point for each pair whose product is nonnegative. So for instance, if n = 3
and your enemy picks 0, −8 and −π, you would pick all possible pairs, {0, −8}, {0, −π} and
{−8, −π}, because all 3 products (0, 0, 8π) are nonnegative. You would get 3 points.
Determine with proof the highest score you can be sure to get against a smart enemy. Your
answer will depend on n.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The product of a pair of numbers with the same sign (both positive or both negative) is positive.
The product of zero and any number is zero, which is non-negative.
A smart enemy will not pick zero, because that will give you a lot of non-negative products.
He/she will have to pick positive and negative numbers.
If  is an even number, is an even number,  , ,
a smart enemy would pick  negative numbers and negative numbers and  positive numbers would give you positive numbers would give you  positive products, positive products,
from 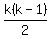 pairs of positive numbers, pairs of positive numbers,
and 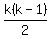 pairs of positive numbers. pairs of positive numbers.
Splitting the negative and positive choices unevenly,
let's say 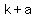 positive numbers and positive numbers and 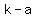 negative numbers, with negative numbers, with  , ,
would give you  positive products, positive products,
and 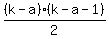 negative products, negative products,
for a total of  , ,
so a smart enemy would not make such a choice.
If one more number could be picked,  , ,
a smart enemy would choose  positive and positive and  negative numbers, negative numbers,
plus an additional number.
The additional number could be positive or negative,
and paired with the  numbers of the same sign, numbers of the same sign,
would give you  additional positive products, additional positive products,
for a total of  points. points.
The formulas work even in the case of
 , where , where  and your score would be and your score would be  , ,
and  , where , where  and your score would be and your score would be  . .
|
|
|