Question 756454: Suppose you are going to list all the subsets,how many subsets are in {3,6,9,12,15,18 ]?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The set {3,6,9,12,15,18} has 6 elements.
NOTE:
There is an issue with the interpretation of what constitutes a subset.
I consider the set {3,6,9,12,15,18} to be a sunset of itself, and I consider the empty set to be a subset too.
So I would have to count all the sets containing 0, 1, 2, 3, 4, 5, and 6 elements from that set. With a different interpretation, the total number of subsets would be less.
There is 1 set with 6 elements, and 1 set with 0 elements.
There are 6 sets with 1 element and 6 sets with 5 elements.
IF YOU KNOW AND UNDERSTAND COMBINATION FORMULAS:
The number of sets of 2, 3, and 4 elements can be calculated as combinations.
There are  sets of 2 elements, sets of 2 elements,
 sets of 3 elements, and sets of 3 elements, and
 sets of 4 elements. sets of 4 elements.
(The same combinatorial formulas could have been used to calculate the number of sets of 0, 1, 5, and 6 elements too).
WITHOUT USING COMBINATION FORMULAS:
When assembling sets of 2 elements, you have 6 choices for the first element, and then 5 elements to chose for the second element, for a total of  possible ordered pairs. However, that would count each set twice, with tje elements in different order. For example, you would have counted the ordered pairs (3,6) and (6,3) as 2 ordered pairs, but they represent just one set, the set {3,6}. So there are only possible ordered pairs. However, that would count each set twice, with tje elements in different order. For example, you would have counted the ordered pairs (3,6) and (6,3) as 2 ordered pairs, but they represent just one set, the set {3,6}. So there are only  sets of 2 elements. sets of 2 elements.
The number of sets of 4 elements is also 15, because each set of 2 elements leaves behind a set of 4 elements.
The number of sets of 3 elements is  because you could make because you could make  ordered triples, but that would count each set of 3 elements ordered triples, but that would count each set of 3 elements  times, because there are times, because there are 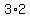 different ways to arrange 3 elements (3 choices for which element is first times 2 choices for which one to place second). different ways to arrange 3 elements (3 choices for which element is first times 2 choices for which one to place second).
ADDING UP:
You can add up the numbers of sets with 0, 1, 2, 3, 4, 5, and 6 elements the simple way:

The fancy way to add would be to add the combinations as a power of a binomial

|
|
|