Question 755607: 36. If the number of subsets with 4 elements of a set A is equal to the number of
subsets with 5 elements of the set, then the number of subsets with 3 elements
of this set is:
(A) 64
(B) 84
(C) 128
(D) none of the above
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website! 36. If the number of subsets with 4 elements of a set A is equal to the number of
subsets with 5 elements of the set, then the number of subsets with 3 elements
of this set is:
One solution would come from the case that if A has 3 or fewer elements, there
would be 0 subsets with 4 elements and 0 subsets with 5 elements, and 0 = 0.
Let's see if there are any other solutions:
If the set contains N elements, then the number of subsets it has with K
elements is C(N,K) =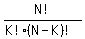 
Suppose set A has N elements, where integer N > 3. Then we have
C(N,4) = C(N,5)
 = 
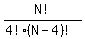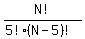Cross multiply
N!5!(N-5)! = N!4!(N-4)!
Divide both sides by N!
5!(N-5)! = 4!(N-4)!
Write out or indicate all the factors of all the factorial:
5·4·3·2·1(N-5)(N-4)(N-3)···1 = 4·3·2·1(N-4)(N-3)···1
Divide both sides through by all the common factors, and we have:
5(N-5) = 1
5N-25 = 1
5N = 26
N =  = 
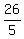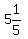That is not an integer, so there are no other cases.
So A has fewer than 4 elements. If A has 3 elements, there is 1
subset, the improper subset A). If A has 2,1,or 0 elements, then
the answer is 0.
Answer: The number of subsets with 3 elements is 0 or 1, or "None of the above".
Edwin
|
|
|
