SOLUTION: List all numbers from the given set B that are members of the given Real Number subset. B={1,√7,-9,0,6/7,√16,0.4 (with a line over the 4),0.24} rational numbers

Algebra ->  Subset -> SOLUTION: List all numbers from the given set B that are members of the given Real Number subset. B={1,√7,-9,0,6/7,√16,0.4 (with a line over the 4),0.24} rational numbers      Log On


   

Question 706338: List all numbers from the given set B that are members of the given Real Number subset.
B={1,√7,-9,0,6/7,√16,0.4 (with a line over the 4),0.24} rational numbers
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
Rational numbers can be expressed as p/q where both p and q are integers and q is not 0.


1 can be expressed as 1/1. It is rational.


sqrt%287%29 is not a rational number. There is no way to express it as p/q - see proof at the end.


9 is rational = 9/1 (any integer is rational). 0 is rational (0/1).


By definition, 6/7 is rational (p=6 and q=7)


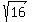sqrt%2816%29 = 4 or -4, so it is rational (4/1 or -4/1).


That line over the 4 means the 4 repeats forever...it is a non terminating decimal that repeats. Non terminating, repeating decimals are rational.


It's easy to find the fraction:


A: x = .4(repeating)


B: 10x = 4.4(repeating) (multiplied A by 10.)


Subtract: B-A = 9x = 4


Solve for x...x=4/9.


.24 is a terminating decimal. Terminating decimals are rational. .24 is 24/100 or simplified 6/25.


The only number from B that isn't a rational number is sqrt%287%29.

Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)



Proof by contradiction: suppose that root 7 (I'll write sqrt(7)) is a rational number, then we can write sqrt(7)=a/b where a and b are integers in their lowest form (ie they are fully cancelled). Then square both sides, you get 7=(a^2)/(b^2) rearranging gives (a^2)=7(b^2). Now consider the prime factors of a and b. Their squares have an even number of prime factors (eg. every prime factor of a is there twice in a squared). So a^2 and b^2 have an even number of prime factors. But 7(b^2) then has an odd number of prime factors. But a^2 can't have an odd and an even number of prime factors by unique factorisation. Contradiction X So root 7 is irrational.