Question 488902: 1. If n(A) = 8, then how many proper subsets does A have?
2. At a local college, a survey was taken to determine where students studied on campus. Of 180 students surveyed, it was determined that:
89 studied in the library
76 studied in the student center
55 studied in both places
Of those interviewed,
a. how many studied in only the library?
b. how many studied in only the student center?
c. how many did not study in either location?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! ANSWER TO PROBLEM NUMBER 1
1. If n(A) = 8, then how many proper subsets does A have?
n(A) = 8 says that the set A has 8 elements.
Here's a definition of elements of a set from Wikipedia.
Writing A = {1, 2, 3, 4 },means that the elements of the set A are the numbers 1, 2, 3 and 4. Sets of elements of A, for example {1, 2}, are subsets of A.
Sets can themselves be elements. For example consider the set B = {1, 2, {3, 4}}. The elements of B are not 1, 2, 3, and 4. Rather, there are only three elements of B, namely the numbers 1 and 2, and the set {3, 4}.
The elements of a set can be anything. For example, C = { red, green, blue }, is the set whose elements are the colors red, green and blue.
Based on this definition, then n(A) = 8 means that the set A consists of 8 subsets.
These would need to be proper subsets since the set itself is not counted as an element of the set.
it was difficult to find an answer that specifically addressed this question so the answer i gave you is pieced together from what i was able to find on the net.
the main source of the information that helped answer the question was wikipedia.
i believe it's true based on the definitions of elements of a set and the excerpt above about how to count elements of a set.
they did not specifically address proper or improper subsets but it is clear that the set itself is not counted as an element of the set, so all elements of the set have to be proper subsets.
an element can be one element or it can be a subset.
an element itself is also considered a subset.
here's the link from wikipedia that clued me in to the fact that a subset is considered an element of a set. you count the set as an element and you do not count the elements within that set.
http://en.wikipedia.org/wiki/Element_%28mathematics%29
the answer to your question is that n(A) tells you the number of proper subsets that are contain in the set A.
this is to the best of my knowledge based on what i learned from wikipedia.
ANSWER TO PROBLEM 2
2. At a local college, a survey was taken to determine where students studied on campus. Of 180 students surveyed, it was determined that:
89 studied in the library
76 studied in the student center
55 studied in both places
Of those interviewed,
a. how many studied in only the library?
b. how many studied in only the student center?
c. how many did not study in either location?
to answer this question, you need to clean up the data set.
that means taking out elements that are in multiple sets and creating a new set that contains the multiples onlyh.
you have 89 studied in the library and 55 studied in both.
remove 55 from 89 to get 34 studied in the library only.
you have 76 studied in the student center and 55 studied in both.
remove 55 from 76 to get 21 studied in the student center only.
add 55 that studied in both.
you have:
34 studied in the library only.
21 studied in the student center only.
55 studied in both.
that's a total of 110
since there were 180 students surveyed, then 180 - 110 = 70 of them studied in neither the library nor the student center.
note that if you did not remove the students that studied both from each category, then the total of students that studied in the library or the student center or both would be equal to 89 + 76 - 55 = 110.
the 55 would have had to be subtracted from the total in order to remove double counting of the 55 who studied in both and were included in both.
by removing them from each category up front, the double counting was avoided and you came up with the same result.
Answer by ikleyn(53431)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. If n(A) = 8, then how many proper subsets does A have?
2. At a local college, a survey was taken to determine where students studied on campus. Of 180 students surveyed, it was determined that:
89 studied in the library
76 studied in the student center
55 studied in both places
Of those interviewed,
a. how many studied in only the library?
b. how many studied in only the student center?
c. how many did not study in either location?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For part (1), tutor @Theo wrote a long essay, but his solution is TOTALLY WRONG.
I came to bring a correct solution to part (1).
It is well known fact that every finite set of 'n' elements has precisely  subsets,
including the empty set and the set itself as a subset.
In our problem, n = 8, so there are subsets,
including the empty set and the set itself as a subset.
In our problem, n = 8, so there are 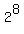 = 256 subsets, as described.
From these 256 subsets, we should exclude one subset, which is the set itself, to get proper subsets.
So, in this problem, there are = 256 subsets, as described.
From these 256 subsets, we should exclude one subset, which is the set itself, to get proper subsets.
So, in this problem, there are 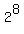 - 1 = 256 - 1 = 255 proper subsets.
ANSWER. Set A has 255 proper subsets. - 1 = 256 - 1 = 255 proper subsets.
ANSWER. Set A has 255 proper subsets.
Solved correctly.
|
|
|