Question 470900: Is the following relation a function? (1, 2), (3, 4), (5, 5)?
Found 2 solutions by nerdybill, MathLover1:
Answer by nerdybill(7384)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Is the following relation a function? (1, 2), (3, 4), (5, 5)
recall: A 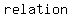 is is 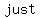 a a 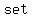 of of 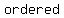 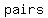 . .
There is absolutely nothing special at all about the numbers that are in a relation. In other words,   of numbers of numbers 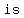 a a 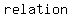 so long as these numbers come in pairs. so long as these numbers come in pairs.
The 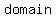 and and 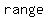 of a relation: of a relation:
The 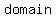 is the set of all the first numbers of the ordered pairs . In other words, the domain is all of the is the set of all the first numbers of the ordered pairs . In other words, the domain is all of the 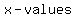 . .
The 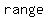 is the set of the second numbers in each pair, or the is the set of the second numbers in each pair, or the 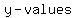 . .
In the relation above the 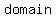 is { 1, 3, 5 } is { 1, 3, 5 }
And the 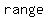 is { 2, 4, 5 } is { 2, 4, 5 }
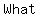 } makes a } makes a 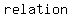 a a  ? ?
 are a are a 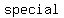 kind of relation . kind of relation .
At first glance, a function looks just like a relation. It's a set of ordered pairs such as { (1, 2), (3, 4), (5, 5)}
Like a relation, a  has a domain and range made up of the has a domain and range made up of the 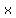 and and  values of ordered pairs. values of ordered pairs.
In mathematics, what distinguishes a function from a relation is that   value in a function has value in a function has 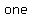 and and   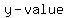 . .
Since relation (1, 2), (3, 4), (5, 5) has 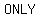   value for value for  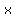 value, this relation value, this relation 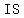 a a  . .
|
|
|