Question 202305This question is from textbook
: Without writing them down, what are the number of subsets of the set A = {a, b, c, d, e}? Of set B = {a, b, c, d, e, f, g, h, i}?
I did not understand this question at all.. I go to school online so I do not get any help of any kind. I read all through my math book but I am so not getting this.. Can you please help??
This question is from textbook
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll do the first one to get you started
Recall, the number of subsets for set A is 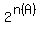 where where 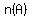 is the number of elements in set A. is the number of elements in set A.
So basically, to find the number of subsets for set A, simply count the number of elements in set A and then raise that number as a power with 2 as the base.
To save ourselves from writing out every subset (and potentially making mistakes), we can simply use the given formula to find the number of possible subsets.
Since n(A) = 5, this means that the possible number of subsets for A is

So there are 32 possible subsets for A
Note: even though set A has 5 elements, this generates 32 possible subsets. So we have saved ourselves from a lot of busy work.
------------------------------------------------------------------------------
Here's a much simpler example:
Let A = {a, b, c}
The subsets of A are:
{a, b, c},
{a, b}, {a, c}, {b, c},
{a}, {b}, {c},
{ }
So there are 8 subsets
Take note that  . In other words, there are 3 elements and 2 cubed gets us 8 possible subsets. . In other words, there are 3 elements and 2 cubed gets us 8 possible subsets.
|
|
|