Question 1204958: In a class of 50 students, 24 like football, 21 basketball and 18 cricket. Six like football and basketball only, 3 like basketball only, 5 like all three games and 14 did not like any of the three games
(i) Illustrate this information on a Venn diagram.
(ii) Find the number of students who like:
(α) football and cricket only;
(β) exactly one of the games.
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
You can put this solution on YOUR website!
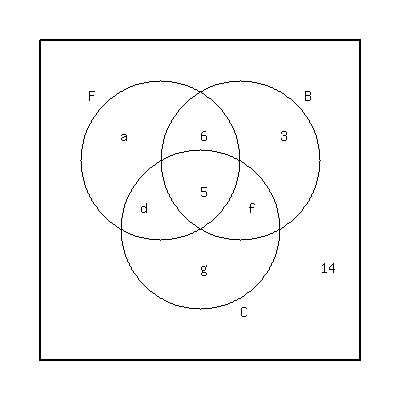
Draw three circles labeled F, B, and C
F = football
B = basketball
C = cricket

We have 3 sports and two options for each (either the person likes it or they don't). That gives 2^3 = 8 distinct regions.
Those 8 regions are labeled 'a' through h
a = those who like football only
b = those who like football and basketball, but not cricket
c = those who like basketball only
etc.
Given Facts
Fact [1]: 50 students
Fact [2]: 24 like football
Fact [3]: 21 like basketball
Fact [4]: 18 like cricket.
Fact [5]: 6 like football and basketball only
Fact [6]: 3 like basketball only
Fact [7]: 5 like all three games
Fact [8]: 14 did not like any of the three games
Facts 5, 6, 7, and 8 lead to b = 6, c = 3, e = 5, and h = 14 in that exact order.
Then we'll use fact [3] to determine that:
b+c+e+f = 21
6+3+5+f = 21
14+f = 21
f = 21-14
f = 7
Next, turn to fact [2] which allows us to say the following
a+b+d+e = 24
a+6+d+5 = 24
a+d+11 = 24
a+d = 24-11
a+d = 13
We'll use this in a substitution step in the next part.
Next we rely on fact [1]
a+b+c+d+e+f+g+h = 50
a+6+3+d+5+7+g+14 = 50
a+d+g+35 = 50
a+d+g = 15
13+g = 15 ...... substitution step
g = 15-13
g = 2
Then we'll turn to fact [4] to say:
d+e+f+g = 18
d+5+7+2 = 18
d+14 = 18
d = 18-14
d = 4
Return to a previous equation to fill in the last missing piece of the puzzle
a+d = 13
a+4 = 13
a = 13-4
a = 9
Summary
a = 9
b = 6
c = 3
d = 4
e = 5
f = 7
g = 2
h = 14
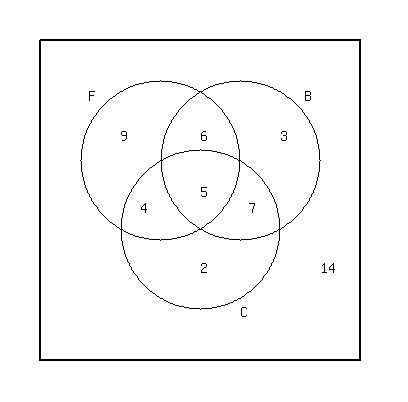
I'll let the student verify this Venn diagram is correct by referring to the 8 facts shown above.
Example:
fact [1] is verified since a+b+c+d+e+f+g+h = 9+6+3+4+5+7+2+14 = 50
The rest of the questions should be fairly straight forward.
I'll let the student take over from here.
Please let me know if you have any questions.
More practice
https://www.algebra.com/algebra/homework/sets-and-operations/sets-and-operations.faq.question.1204589.html
|
|
|