|
Tutors Answer Your Questions about Square-cubic-other-roots (FREE)
Question 1181912: Al-khwarizmi solved all quadratic equations by reducing them to one of six standard forms, which were then easily solvable. He described the standard forms in terms of “squares”,”roots”, and “numbers”. Here are al-khwarizmis six standard forms.
1. Squares equal to roots(example:ax^2=bx)
2. Squares equal to numbers(example:ax^2=c)
3.roots equal to numbers(example:bx=c)
4.squares and roots equal to numbers (example:ax^2+bx=c)
5. Squares and numbers equal to roots (example: ax^2+c=bx)
6.roots and numbers equal to tot squares(example:ax^2=bx+c)
Which method would you use to solve each of the six forms? Why would you use that method?
Write a quadratic equation that can be reduced to one of al-khwarizmis six forms.
Click here to see answer by CPhill(1959)   |
Question 1183944: Al-Khwarizmi solved all quadratic equations by reducing them to one of six standard forms, which were then easily solvable. He described the standard forms in terms of "squares," "roots," and "numbers." Here are al-Khwarizmi's six standard forms:
squares equal to roots (Example: ax2= bx
a x squared equals space b x)
squares equal to numbers (Example: ax2= c
a x squared equals space c)
roots equal to numbers (Example: bx=c
b x equals c)
squares and roots equal to numbers (Example: ax2+bx=c
a x squared plus b x equals c)
squares and numbers equal to roots (Example: ax2+c=bx
a x squared plus c equals b x)
roots and numbers equal tot squares (Example: ax2=bx+c
a x squared equals b x plus c)
Activity Instructions
• Which method would you use to solve each of the six forms? Why would you use that method?
• Write a quadratic equation that can be reduced to one of al-Khwarizmi's six forms.
Click here to see answer by CPhill(1959)   |
Question 1207360: Rationalize the denominator.
Let cr = cube root.
5/(cr(2))
Let me see.
5/(cr(2)) • (cr(2))/(cr(2))
5(cr(2))/(2)
The book's answer is different.
P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?
Click here to see answer by MathTherapy(10552)   |
Question 1207360: Rationalize the denominator.
Let cr = cube root.
5/(cr(2))
Let me see.
5/(cr(2)) • (cr(2))/(cr(2))
5(cr(2))/(2)
The book's answer is different.
P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?
Click here to see answer by greenestamps(13200)   |
Question 1207360: Rationalize the denominator.
Let cr = cube root.
5/(cr(2))
Let me see.
5/(cr(2)) • (cr(2))/(cr(2))
5(cr(2))/(2)
The book's answer is different.
P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?
Click here to see answer by Edwin McCravy(20059)   |
Question 1207360: Rationalize the denominator.
Let cr = cube root.
5/(cr(2))
Let me see.
5/(cr(2)) • (cr(2))/(cr(2))
5(cr(2))/(2)
The book's answer is different.
P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?
Click here to see answer by math_tutor2020(3817)  |
Question 1207360: Rationalize the denominator.
Let cr = cube root.
5/(cr(2))
Let me see.
5/(cr(2)) • (cr(2))/(cr(2))
5(cr(2))/(2)
The book's answer is different.
P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?
Click here to see answer by mananth(16946)   |
Question 1206526: Below are the multiplication problems.
1). 17 x 23 ( I was informed to subtract 9 from 400).
2. 23 x 37 ( I was informed to subtract 49 from 900).
3). 18 x 30 ( I was informed to subtract 36 from 576).
What type of math strategy is this?
Click here to see answer by josgarithmetic(39620)  |
Question 1206526: Below are the multiplication problems.
1). 17 x 23 ( I was informed to subtract 9 from 400).
2. 23 x 37 ( I was informed to subtract 49 from 900).
3). 18 x 30 ( I was informed to subtract 36 from 576).
What type of math strategy is this?
Click here to see answer by greenestamps(13200)   |
Question 1206526: Below are the multiplication problems.
1). 17 x 23 ( I was informed to subtract 9 from 400).
2. 23 x 37 ( I was informed to subtract 49 from 900).
3). 18 x 30 ( I was informed to subtract 36 from 576).
What type of math strategy is this?
Click here to see answer by math_tutor2020(3817)  |
Question 1064008: Joe is trying to soup up his dragster. He knows that the time needed for the car to go from 0 to 100 miles per hour varies inversely with the car's horsepower. At 200 horsepower, the car can go from 0 to 100 mph in 12 seconds. How long should the car take if he can increase the horsepower to 240 hp?
Click here to see answer by mananth(16946)   |
Question 1202969: Solve the following by either factoring, square root method, or quadratic formula. For each question determine which is the best method to use and why. Then solve the equation showing all work, and simplify your answers fully. Keep in mind that the quadratic formula is not always the most efficient method.
21-3(t-2)^2=9
x^2 + 12x-20=0
(x+3)(x-6)=-8
Click here to see answer by greenestamps(13200)   |
Question 1202968: Evaluate the three radicals. Though they look similar, each one is different.
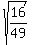
- 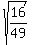

-
Which of the above square roots can be simplified with a real number answer and what is the simplified value?
Which of the above square roots cannot be simplified and why can they not be simplified?
Click here to see answer by math_tutor2020(3817)  |
Question 1201162: This is probably a really stupid question. Please bear with me.
I was reading this article
https://www.mathsisfun.com/algebra/square-root.html
It's helping me learn a lot. The professor mentions the rule sqrt(xy) = sqrt(x)sqrt(y) then says "but only when x and y are both greater than or equal to 0"
But then there's this article
https://www.mathsisfun.com/numbers/imaginary-numbers.html
She or he breaks up the -9 into 9 x -1 and uses the square root rule only meant for positive numbers.
What gives? Why is the -1 allowed?
I don't understand sqrt(xy) = sqrt(x)sqrt(y) for x > 0 y > 0 but it clearly works(?) for negative numbers also.
I suppose I don't really understand imaginary numbers too much. I appreciate you reading this and helping me out.
Click here to see answer by greenestamps(13200)   |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380
|
| |



