|
Tutors Answer Your Questions about Square-cubic-other-roots (FREE)
Question 1181912: Al-khwarizmi solved all quadratic equations by reducing them to one of six standard forms, which were then easily solvable. He described the standard forms in terms of “squares”,”roots”, and “numbers”. Here are al-khwarizmis six standard forms.
1. Squares equal to roots(example:ax^2=bx)
2. Squares equal to numbers(example:ax^2=c)
3.roots equal to numbers(example:bx=c)
4.squares and roots equal to numbers (example:ax^2+bx=c)
5. Squares and numbers equal to roots (example: ax^2+c=bx)
6.roots and numbers equal to tot squares(example:ax^2=bx+c)
Which method would you use to solve each of the six forms? Why would you use that method?
Write a quadratic equation that can be reduced to one of al-khwarizmis six forms.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a breakdown of how to solve each of Al-Khwarizmi's six forms, along with explanations:
**1. Squares equal to roots (ax² = bx)**
* **Method:** Divide both sides by *x* (assuming *x* is not zero). This simplifies the equation to *ax = b*, which can be solved directly for *x*.
* **Why:** Dividing by *x* reduces the quadratic to a linear equation, which is much easier to solve. We must consider the case where *x* = 0 separately, as it is a solution to the original equation.
**2. Squares equal to numbers (ax² = c)**
* **Method:** Divide both sides by *a*, then take the square root of both sides. Remember to consider both the positive and negative square roots. This gives *x* = ±√(c/a).
* **Why:** Taking the square root isolates *x*. The ± is crucial because both positive and negative values, when squared, can equal *c/a*.
**3. Roots equal to numbers (bx = c)**
* **Method:** Divide both sides by *b*. This gives *x = c/b*.
* **Why:** This is already a linear equation; dividing by *b* directly solves for *x*.
**4. Squares and roots equal to numbers (ax² + bx = c)**
* **Method:** Complete the square. Divide the entire equation by *a* to get *x² + (b/a)x = c/a*. Take half of the coefficient of *x* (which is *b/2a*), square it (*b²/4a²*), and add it to both sides. This creates a perfect square on the left side: *x² + (b/a)x + b²/4a² = c/a + b²/4a²*. Rewrite the left side as *(x + b/2a)² = c/a + b²/4a²*. Then take the square root of both sides, remembering the ±, and solve for *x*.
* **Why:** Completing the square transforms the quadratic into a form where taking the square root isolates *x*.
**5. Squares and numbers equal to roots (ax² + c = bx)**
* **Method:** Rearrange the equation to get it into the standard form for completing the square (ax² - bx + c = 0). Then, follow the same "completing the square" steps as in form 4.
* **Why:** Same as form 4, completing the square makes the equation solvable by taking the square root.
**6. Roots and numbers equal to squares (ax² = bx + c)**
* **Method:** Rewrite as ax² - bx - c = 0. Then, again, complete the square as in forms 4 and 5.
* **Why:** Consistent with the previous forms, completing the square is the key to isolating x.
**Example Quadratic Equation:**
The equation 3x² + 5 = 7x can be reduced to Al-Khwarizmi's form 5 (Squares and numbers equal to roots). Subtracting 7x from both sides gives 3x² - 7x + 5 = 0.
Question 1209713: Let a and b be integer such that (2 + sqrt(5))(137) = a + b sqrt(5). Compute a^2 - 5b^2.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1183944: Al-Khwarizmi solved all quadratic equations by reducing them to one of six standard forms, which were then easily solvable. He described the standard forms in terms of "squares," "roots," and "numbers." Here are al-Khwarizmi's six standard forms:
squares equal to roots (Example: ax2= bx
a x squared equals space b x)
squares equal to numbers (Example: ax2= c
a x squared equals space c)
roots equal to numbers (Example: bx=c
b x equals c)
squares and roots equal to numbers (Example: ax2+bx=c
a x squared plus b x equals c)
squares and numbers equal to roots (Example: ax2+c=bx
a x squared plus c equals b x)
roots and numbers equal tot squares (Example: ax2=bx+c
a x squared equals b x plus c)
Activity Instructions
• Which method would you use to solve each of the six forms? Why would you use that method?
• Write a quadratic equation that can be reduced to one of al-Khwarizmi's six forms.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down each of al-Khwarizmi's six forms and discuss appropriate solution methods, along with example equations.
**1. Squares equal to roots (ax² = bx):**
* **Method:** Divide both sides by 'x' (assuming x ≠ 0) to get ax = b, then solve for x: x = b/a. We can also factor it as x(ax-b)=0, so x=0 or x=b/a.
* **Why:** This simplifies the quadratic to a linear equation, which is easy to solve.
* **Example:** 3x² = 12x => 3x = 12 => x = 4 (or x=0).
**2. Squares equal to numbers (ax² = c):**
* **Method:** Divide both sides by 'a' to get x² = c/a, then take the square root of both sides: x = ±√(c/a).
* **Why:** This isolates x², allowing us to directly find the value(s) of x using the inverse operation (square root).
* **Example:** 5x² = 20 => x² = 4 => x = ±2.
**3. Roots equal to numbers (bx = c):**
* **Method:** Divide both sides by 'b' to get x = c/b.
* **Why:** This is already a linear equation; one simple division gives the solution.
* **Example:** 7x = 21 => x = 3.
**4. Squares and roots equal to numbers (ax² + bx = c):**
* **Method:** This is the classic quadratic equation form. Use the quadratic formula: x = (-b ± √(b² - 4ac)) / 2a. Completing the square also works.
* **Why:** The quadratic formula provides a general solution for this type of equation.
* **Example:** 2x² + 5x = 12.
**5. Squares and numbers equal to roots (ax² + c = bx):**
* **Method:** Rearrange the equation to the standard quadratic form (ax² - bx + c = 0) and then use the quadratic formula: x = (b ± √(b² - 4ac)) / 2a. Completing the square also works.
* **Why:** Similar to the previous case, the quadratic formula is a direct way to find the solution(s).
* **Example:** 3x² + 4 = 8x => 3x² - 8x + 4 = 0.
**6. Roots and numbers equal to squares (ax² = bx + c):**
* **Method:** Rearrange the equation to the standard quadratic form (ax² - bx - c = 0) and use the quadratic formula: x = (b ± √(b² + 4ac)) / 2a. Completing the square also works.
* **Why:** Again, the quadratic formula provides a general solution.
* **Example:** 2x² = 5x + 3 => 2x² - 5x - 3 = 0.
Question 1209707: Let (2 + \sqrt{5})(137) = a + b \sqrt{5}, where a and b are integers. Compute a^2 - 5b^2.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the given equation be
$$(2 + \sqrt{5})(137) = a + b\sqrt{5}$$
where $a$ and $b$ are integers.
Expanding the left side, we have
$$2(137) + 137\sqrt{5} = a + b\sqrt{5}$$
$$274 + 137\sqrt{5} = a + b\sqrt{5}$$
Comparing the rational and irrational parts, we get $a = 274$ and $b = 137$.
We are asked to compute $a^2 - 5b^2$.
$$a^2 - 5b^2 = (274)^2 - 5(137)^2 = (274)^2 - 5(137)^2$$
$$= (2 \cdot 137)^2 - 5(137)^2 = 4(137)^2 - 5(137)^2 = (4-5)(137)^2 = -1(137)^2 = -18769$$
Therefore, $a^2 - 5b^2 = -18769$.
Final Answer: The final answer is $\boxed{-18769}$
Question 1209597: Find all values of x satisfying
sqrt(4x - 3) + 40/sqrt(4x - 3) = 12x + 14.
Answer by ikleyn(52800)   (Show Source): (Show Source):
Question 1209551: I have to solve an square root without a calculator. It has to be in a(square root symbol) b. Help please!
Found 4 solutions by ikleyn, mccravyedwin, Edwin McCravy, math_tutor2020:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I have to  compute compute  a square root without a calculator. a square root without a calculator.
It has to be in a(square root symbol) = b. Help please!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I asked Google with these keywords "algorithm of finding square root of an integer number manually".
Google knows everything, the major thing is to ask a right question.
This time Google provided these links:
(a) wording description by Artificial Intelligence
https://www.google.com/search?q=algorithm+of+finding+square+root+of+an+integer+number+manually&rlz=1C1CHBF_enUS1071US1071&oq=algorithm+of+finding+square+root+of+an+integer+number+manually&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCjM3MjY3ajBqMTWoAgiwAgE&sourceid=chrome&ie=UTF-8
(b) Video-lessons
https://www.youtube.com/watch?v=HBdVVFqTrUU
https://www.youtube.com/watch?v=x4D5bPqONAE
It is how my teachers taught me many years ago, in my 6-th grade.
To be honest, after learning this algorithm in school, I did not use it in my life NO ONE single time.
(Although all my life was making scientific computing).
So, in my view, this knowledge does belong to the category of absolutely useless subjects.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here's the square root of a perfect square by the "ancient" method.
2 9 4
√8 64 36
4
40|4 64
49|4 41
580|23 36
584|23 36
0
√(86436) = 294
Edwin
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is how I was taught to take the square root of a number back in about 6th
grade before anybody had heard of an electronic computer or calculator. It
reminds one of the algorithm of long division, but it's lots more complicated.
See if you can figure out how we took the square root of 2 back in 1940-1950.
1. 4 1 4 2
√2. 00 00 00 00 <--you can keep adding pairs " 00 "
1
20| 1 00
24| 96
280| 4 00
281| 281
2820| 119 00
2824| 112 96
28280| 6 04 00
28284| 5 75 68
28 32
Edwin
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1209102: Arrange the following numbers in increasing order (smallest first, biggest last):
A = 2^(1/2)*4^(1/6)*8^(1/3)
B = 12*128
C = 8^(1/5)^2*8^(1/5)^3
D = 4*(-1)*2*(-1)*8*(-1)
E = 2^(1/2)*3*4^(1/4)
Found 3 solutions by MathTherapy, mccravyedwin, ikleyn:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I think that every person should care about his/her brain/mind and time
and do not perform such idiotic assignments by hands.
It is much better to spend your time for some more educative reading,
studying, exercising, walking, sleeping etc.
Question 1209119: The difference of two positive numbers is 99. The numbers multiply to 630. What is the sum of their squares?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x^2 + y^2 = x^2 -2xy + y^2 + 2xy = (x^2 -2xy + y^2) + 2xy = (x-y)^2 + 2xy = 99^2 + 2*630 = 11061. ANSWER
Solved.
The idea of the solution is to present the sum of the squares (the desired value)
via given information by a simplest way, using well known identities.
It is how this problem is designed and how to it is expected to be solved.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 11061
Explanation
Let's say x and y are the two numbers where x is the bigger value.
x > y and both are larger than 0
xy = 630 is the product of the values which will be useful later.
x-y = 99 since the two numbers are 99 units apart, ie. their difference is 99
Since your teacher wants to know the sum of the squares, let's square both sides to see what happens.
(x-y)^2 = 99^2
x^2-2xy+y^2 = 9801
x^2+y^2-2xy = 9801
x^2+y^2-2*(xy) = 9801
x^2+y^2-2*(630) = 9801 ..... plug in xy = 630
x^2+y^2-1260 = 9801
x^2+y^2 = 9801+1260
x^2+y^2 = 11061 is the sum of the squares of the two mystery numbers.
--------------------------------------------------------------------------
Notice how we don't need to find x and y themselves.
However, if you wanted to, you could follow that pathway.
Ignore this section if you prefer the previous method shown above.
x-y = 99 can be rearranged to y = x-99
Plug that into the other equation to get,
xy = 630
x*( y ) = 630
x*(x-99) = 630
x^2-99x = 630
x^2-99x-630 = 0
Then apply the quadratic formula to get the roots x = -6 and x = 105.
I'll let the student handle the scratch work.
We ignore x = -6 because the instructions mention the numbers are positive.
If x = 105 then y = x-99 = 105-99 = 6.
We determine that x = 105 and y = 6 are the two mystery numbers.
The scratch work shown below confirms we have the correct x,y pairing.
x-y = 105-6 = 99
x*y = 105*6 = 630 Then,
x^2+y^2 = 105^2+6^2 = 11061 is the final answer.
Question 1209035: What is the smallest positive integer n such that \sqrt[4]{675 + n} is an integer?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We want 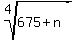 to be an integer. to be an integer.
5^4 = 625, which is less than 675.
6^4 = 1296, which is greater than 675.
675+n = 1296
n = 1296-675 = 621
ANSWER: 621
Question 1208754: Find the range of y = sqrtx - 2}.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Assuming the function is y = sqrt(x-2)....
Any square root function always returns a value that is greater than or equal to 0.
For this function, the value is clearly 0 when x is 2; and there is no restriction on how large x can be, so
ANSWER: [0,infinity)
Question 1208359: Simplify sqrt{4x^3•9y^5}.
Found 4 solutions by ikleyn, mccravyedwin, math_tutor2020, josgarithmetic:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Simplify sqrt{4x^3•9y^5}.
~~~~~~~~~~~~~~~
This problem is a TRAP, and both tutors Edwin and @math_tutor2020 fell into it.
To solve the problem correctly, we should reveal a context accurately.
The domain, i.e. the area where this expression is defined, is the set of points (x,y)
in the 1st quadrant or in the 3rd quadrant. It means that the domain is the union of both quadrants.
In other words x >= 0, y >= 0 are allowed under the square root; or x <= 0, y <= 0 simultaneously.
But x and y of different signs are not allowed.
Second note is that when square root is considered as a function or as an expression,
by a commonly accepted agreement, it is considered as non-negative value or expression.
Again, it is the common agreement for square root, when it is considered
as an expression of variables, that its output values are non-negative.
Next, the first move is to write 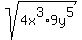 = =  . (1)
But this expression is only half-right. On the other half it is WRONG.
It is wrong in 3rd quadrant. Numerical values under the square root are non-negative there.
It is good, since we can extract the square root then.
But the values of the simplified expression (1) will be negative in 3rd quadrant,
which is not consistent with the agreement mentioned above.
Therefore, we should write (1) in MODIFIED form . (1)
But this expression is only half-right. On the other half it is WRONG.
It is wrong in 3rd quadrant. Numerical values under the square root are non-negative there.
It is good, since we can extract the square root then.
But the values of the simplified expression (1) will be negative in 3rd quadrant,
which is not consistent with the agreement mentioned above.
Therefore, we should write (1) in MODIFIED form
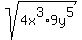 = = 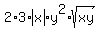 = = 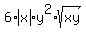 , (2)
placing x under the absolute value sign.
In this form (2), it is consistent with (1) in the first quadrant and provides non-negative output
in the third quadrant.
ANSWER. , (2)
placing x under the absolute value sign.
In this form (2), it is consistent with (1) in the first quadrant and provides non-negative output
in the third quadrant.
ANSWER. 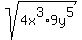 } is } is 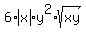 in the 1st and 3rd quadrants. in the 1st and 3rd quadrants.
Solved. The correct answer is expression (2).
---------------------
For your info and for info of the tutors, practically all without exceptions fall into this trap,
if they are unfamiliar with this logic/reasoning for advance, until somebody explains a right way reasoning.
So, to get the right answer to this problem and to many other similar problems,
you need accurately determine the domain, accurately reveal the context and accurately
adopt the output expression in order for to have positive values of the final square root expression over the entire domain.
It is the KEY to solving such problems.
The key point to understand is that when square root of a non-negative number is considered,
it has two values - one positive and one negative, opposite to the positive value.
On contrary, when square root of a function or of an expression is considered,
the common agreement is that in this situation the output (the result of applying square root) must be non-negative.
It requires special cares in the solution.
I think that 99% (or 99.99%) of contemporary people/students/teachers don't know this wisdom.
But it is how my teachers taught us in my high school years.
By the way, at the time, when I entered the university, we were oblige to pass
entering exams; two of the exams were in Math, written and oral.
The competition for admission was 10:1; the participants were the best mathematical minds
of my generation from the entire country, and those who did not know (did not have) this wisdom/understanding
or other similar wisdoms/knowledge/technique/skills, had no chance to pass.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
And the last argument, to make you smile and to convince you in full.
I asked my Google browser " simplify 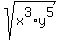 ". ".
It ran its AI, which generated the solution and the answer 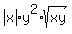 , ,
in precise accordance with my logic.
The link is
https://www.google.com/search?q=simplify+sqrt%28x%5E3*y%5E5%29&sca_esv=d744b37d0a57b190&sca_upv=1&rlz=1C1CHBF_enUS1071US1071&sxsrf=ADLYWIJQbRLqpb3gj7WgO1QlYzC1Q4VUsg%3A1727563466077&ei=yob4ZtKwBI_n0PEP1paqoQc&ved=0ahUKEwjSveO12-aIAxWPMzQIHVaLKnQQ4dUDCA8&uact=5&oq=simplify+sqrt%28x%5E3*y%5E5%29&gs_lp=Egxnd3Mtd2l6LXNlcnAiFnNpbXBsaWZ5IHNxcnQoeF4zKnleNSkyBRAhGJ8FMgUQIRifBTIFECEYnwUyBRAhGJ8FMgUQIRifBTIFECEYnwUyBRAhGJ8FMgUQIRifBUizOlDvDVj9MHABeAGQAQCYAWqgAcEEqgEDNS4xuAEDyAEA-AEBmAIHoALiBMICChAAGLADGNYEGEfCAgYQABgWGB7CAgsQABiABBiGAxiKBcICCBAAGIAEGKIEmAMAiAYBkAYIkgcDNC4zoAeuLg&sclient=gws-wiz-serp
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Question 1208358: Why does √xy = √x√y?
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Question 1208360: Simplify cube root{27x^3•y^3•z^5}.
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Question 1207378: Give an example to show that sqrt{a^2} is not equal to a. Use it to explain why sqrt{a^2} = |a|.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Question 1207360: Rationalize the denominator.
Let cr = cube root.
5/(cr(2))
Let me see.
5/(cr(2)) • (cr(2))/(cr(2))
5(cr(2))/(2)
The book's answer is different.
P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?
Found 5 solutions by MathTherapy, greenestamps, Edwin McCravy, math_tutor2020, mananth:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll go ahead and use your notation of cr(2) to represent the cube root of 2.
The given expression has cr(2) in the denominator. In the work you show, you multiplied numerator and denominator by cr(2). But cr(2) times cr(2) does not rationalize the denominator. You need to multiply numerator and denominator by cr(2) twice to make the denominator rational.
(5/cr(2)*(cr(2)/cr(2))*(cr(2)/cr(2)) = (5*cr(2)*cr(2))/2 = 5cr(4)/2
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1207287: What is the simplified version of √150y⁴
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1206526: Below are the multiplication problems.
1). 17 x 23 ( I was informed to subtract 9 from 400).
2. 23 x 37 ( I was informed to subtract 49 from 900).
3). 18 x 30 ( I was informed to subtract 36 from 576).
What type of math strategy is this?
Found 3 solutions by josgarithmetic, greenestamps, math_tutor2020:
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
These are all examples of a strategy for mental calculations based on the pattern (A+B)(A-B)=A^2-B^2
17*23 = (20-3)(20+3) = 20^2-3^2 = 400-9
23*37 = (30-7)(30+7) = 30^2-7^2 = 900-49
18*30 = (24-6)(24+6) = 576-36 = 540
While that strategy can of course be used on the last example, it is not a good place to use it, since 18*30 is much more easily calculated as 18*3*10.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll focus on problem 1 only.
Note how 20 is the midpoint of 17 and 23.
midpoint = (a+b)/2
17 x 23 = (20 - 3) x (20 + 3)
17 x 23 = 20^2 - 3^2
17 x 23 = 400 - 9
17 x 23 = 391
I used the difference of squares rule.
The other two problems will use a similar approach.
Question 1064008: Joe is trying to soup up his dragster. He knows that the time needed for the car to go from 0 to 100 miles per hour varies inversely with the car's horsepower. At 200 horsepower, the car can go from 0 to 100 mph in 12 seconds. How long should the car take if he can increase the horsepower to 240 hp?
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! 

p=200, t=12 s
12= k*1/200
k=2400
Now
P=240, t=?
t= 2400*(1/240)
t= 10s
The car should take 10 seconds to go from 0 to 100 mph at 240 hp
Question 1206295: all i need is # of roots, range, and axis of symmetry for the problem
f(x)=-x^2-2x+3
PLEASE and Thank You
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Question 1205842: Evaluate sqrt(5 + sqrt(5^2 + sqrt(5^4 + sqrt(5^8 + ...))))
Answer by ikleyn(52800)   (Show Source): (Show Source):
Question 1203597: Consider the parent function  . What parameters (a, k, d, c) affect the domain of g(x) = af[k(x-d)]+c? Please explain. . What parameters (a, k, d, c) affect the domain of g(x) = af[k(x-d)]+c? Please explain.
Found 2 solutions by Edwin McCravy, MathLover1:
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider the parent function  . What parameters (a, k, d, c) affect the domain of g(x) = af[k(x-d)]+c? Please explain. . What parameters (a, k, d, c) affect the domain of g(x) = af[k(x-d)]+c? Please explain.
What is done to the variable only possibly affects the domain.
What is done to the entire function only possibly affects the range.
Only d and k are things done to the variable x only, so they possibly affect the
domain.
Only a and c are things done to the entire function, so they possibly affect the
range.
Explanation:
We will assume that a, k, d, c are all positive.
If we do something to the VARIABLE ONLY, it's a HORIZONTAL change.
If we do something to the ENTIRE FUNCTION, it's a VERTICAL change.
We must always do all HORIZONTAL CHANGES first. That is, we must do something to
the VARIABLE first if there is anything to do to it. Only when we have done
everything HORIZONTAL to the VARIABLE ONLY, will we proceed to do something
VERTICAL to the ENTIRE FUNCTION.
Horizontal changes do the OPPOSITE to "what you would expect":
Horizontal changes by ADDING to the variable move the curve LEFTWARD horizontally.
Horizontal changes with SUBTRACTING from the variable move the curve RIGHTWARD
horizontally.
Horizontal changes with MULTIPLYING the variable by numbers > 1 SHRINK the
graph horizontally.
Horizontal changes with MULTIPLYING by numbers < 1 STRETCH the graph
horizontally.
VERTICAL changes do "what you would expect":
Vertical changes with ADDITION to the entire function move the curve UPWARD
vertically.
Vertical changes with SUBTRACTION from the entire function move the curve
DOWNWARD vertically.
Vertical changes with MULTIPLICATION of the entire function by numbers > 1
stretch the graph vertically.
Vertical changes with MULTIPLICATION of the entire function by numbers < 1
shrink the graph vertically.
Here is the order in which we will proceed from f(x) to g(x)
Notice that the usual order of operations are followed, multiplication is done
before addition and subtraction.




 Start with the parent function
Start with the parent function  We do something to the variables first, which will result in horizontal changes.
First we do something to the variable x only by multiplying x by k, so
it will do the opposite of what you might think:
We do something to the variables first, which will result in horizontal changes.
First we do something to the variable x only by multiplying x by k, so
it will do the opposite of what you might think:
 That shrinks the graph horizontally by a factor of 1/k if k > 1 or stretches it
by a factor of k if k < 1.
Next, we again do something to the variable x only by subtracting d from the
variable x, so again it will do the opposite of what you might think:
That shrinks the graph horizontally by a factor of 1/k if k > 1 or stretches it
by a factor of k if k < 1.
Next, we again do something to the variable x only by subtracting d from the
variable x, so again it will do the opposite of what you might think:
 That shifts the graph horizontally TO THE RIGHT by a distance of d units.
We have done everything to the variable. So now we do something to the ENTIRE FUNCTION.
Now we multiply the ENTIRE FUNCTION by "a". Now what we do will be "what you
would expect":
That shifts the graph horizontally TO THE RIGHT by a distance of d units.
We have done everything to the variable. So now we do something to the ENTIRE FUNCTION.
Now we multiply the ENTIRE FUNCTION by "a". Now what we do will be "what you
would expect":
 This stretches the graph by a factor of 'a' if a > 1 and skrinks it vertically
by a factor of 1/a if a < 1.
Finally we add 'c' to the ENTIRE FUNCTION. This does "what you would expect".
It shifts the entire graph vertically UPWARD by 'c' units.
This stretches the graph by a factor of 'a' if a > 1 and skrinks it vertically
by a factor of 1/a if a < 1.
Finally we add 'c' to the ENTIRE FUNCTION. This does "what you would expect".
It shifts the entire graph vertically UPWARD by 'c' units.
 Edwin
Edwin
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1202969: Solve the following by either factoring, square root method, or quadratic formula. For each question determine which is the best method to use and why. Then solve the equation showing all work, and simplify your answers fully. Keep in mind that the quadratic formula is not always the most efficient method.
21-3(t-2)^2=9
x^2 + 12x-20=0
(x+3)(x-6)=-8
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1202968: Evaluate the three radicals. Though they look similar, each one is different.
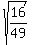
- 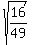

-
Which of the above square roots can be simplified with a real number answer and what is the simplified value?
Which of the above square roots cannot be simplified and why can they not be simplified?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1198694: The sum of cube root of two numbers is 128,while the sum of the reciprocals of their cubes is 2. What are thosw two numbers...Thank You..
Found 2 solutions by ikleyn, mananth:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The numbers that @mananth announced as solutions
x = 32^3, y = 96^3
do not satisfy equation
 + + 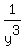 = 2. = 2.
Therefore, what he calls " the solution ", is not a solution, at all.
It looks like he is unfamiliar with the conception of checking a solution, at all.
Absolutely mathematically illiterate person.
But wants very much to teach others.
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1201162: This is probably a really stupid question. Please bear with me.
I was reading this article
https://www.mathsisfun.com/algebra/square-root.html
It's helping me learn a lot. The professor mentions the rule sqrt(xy) = sqrt(x)sqrt(y) then says "but only when x and y are both greater than or equal to 0"
But then there's this article
https://www.mathsisfun.com/numbers/imaginary-numbers.html
She or he breaks up the -9 into 9 x -1 and uses the square root rule only meant for positive numbers.
What gives? Why is the -1 allowed?
I don't understand sqrt(xy) = sqrt(x)sqrt(y) for x > 0 y > 0 but it clearly works(?) for negative numbers also.
I suppose I don't really understand imaginary numbers too much. I appreciate you reading this and helping me out.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1199797: Factor 216x^3-27y^3
Found 2 solutions by MathTherapy, josgarithmetic:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Factor 216x^3-27y^3
STEP 1: Factor out a GCF, if there's one! There's one.
STEP 2: Apply the DIFFERENCE of CUBES to the NEW binomial.
STEP 3: Whatever factors you get in Step 2, check to make sure that they are PRIME.
If so, you're done. If not, then continue factoring until the binomial is COMPLETELY factored.
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Question 1199805: Determine the cubic equation that has zeros at -8 , -4 and 13, if f(-10)=-138
Justify your answer
Thank you so much
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380
|
| |



