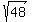 Start with the given expression Start with the given expression
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. When you take the square root of this perfect square, you will get a rational number.
So let's list the factors of 48
Factors:
1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Notice how 16 is the largest perfect square, so lets factor 48 into 16*3
 Factor 48 into 16*3 Factor 48 into 16*3
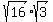 Break up the square roots using the identity Break up the square roots using the identity 
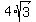 Take the square root of the perfect square 16 to get 4 Take the square root of the perfect square 16 to get 4
So the expression 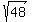 simplifies to simplifies to 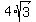
----------------------------
Check:
Notice if we evaluate the square root of 48 with a calculator we get

and if we evaluate 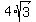 we get we get

This shows that  . So this verifies our answer . So this verifies our answer |