SOLUTION: please help me to solve this problem prove it roots of of this equation ; ( x^2+(mx+c)^2=a^2) will be equal if (c^2=a^2(1+m^2))

roots of of this equation ; ( x^2+(mx+c)^2=a^2) will be equal if (c^2=a^2(1+m^2))

Expanding the given equation


Rewriting it in standard quadratic form


This is of the form A*x^2 + B*x + C = 0 (I am writing A, B, C in uppercase so 
that you don't confuse them with the a,b,c given in the problem)

The roots of the quadratic are equal if the "discriminant" is 0

Discriminant = 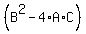 -----> (1)

Here A = (1 + m^2) ---> coefficient of x^2 term
B = 2*m*c  -----> coefficient of x term
C = c^2 - a^2 -----> constant term

Discriminant(substituting for A,B,C in eqn (1))

= 


 -> proved!

Hope you got it :)