SOLUTION: Show me x squared + x cubed = 810

x² + x³ = 810

Rearrange in descending order:

x³ + x² - 810 = 0

If it has any rational solutions, they will be ± factors
of 810, which are:

±1, ±2, ±3, ±5, ±6, ±9, ±10, ±15, ±18, ±27, ±30, ±45,
±54, ±81, ±90, ±135, ±162, ±270, ±405, ±810

It has one sign change so it has 1 positive solution.
So we'll try the positive values with synthetic division.
Notice that we have to put in a place holder for there
is no x term, so we consider the equation as 
x³ + x² + 0x - 810 = 0

We try 1:

1|1  1  0  -810
 |   1  2     2  
  1  2  2  -808  No

We try 2:

2|1  1  0  -810
 |   2  6    12  
  1  3  6  -798  No

We try 3:

3|1  1   0  -810
 |   3  12    36  
  1  4  12  -774  No

We try 5:

5|1  1   0  -810
 |   5  30   150  
  1  6  30  -660  No 

We try 6:

6|1  1   0  -810
 |   6  42   252  
  1  7  42  -558  No

We try 9:

9|1  1   0  -810
 |   9  90   810  
  1 10  90     0  YES!

So x³ + x² - 810 = 0 factors as

(x - 9)(x² + 10x + 90) = 0

We use the zero-factor principle:

x - 9 = 0;  x² + 10x + 90
    x = 9;  x =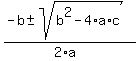 
            x = 
            x =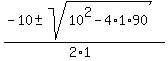 
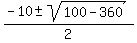            x =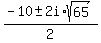 
            x = 
            x =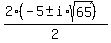 
            x = 
            x =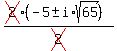 
            x = 
            x =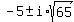 

Three solutions, one real and two imaginary:

9, 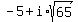, and 

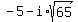Edwin