|
Question 635765: Find the following. Assume that variables can represent any real number.
√(a+7)^2 =
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First a quick review.- Every positive number has two square roots, a positive square root and a negative square root. For example, 25 has 5 and -5 as square roots.
- The square root symbol is used only to express the positive square root. To express the negative square root you put a minus in front of the square root symbol. To express both square roots you put the "plus or minus" symbol in front. For example:


+ refers to both 5 and -5. refers to both 5 and -5. - The expression inside the square root symbol, called the radicand, is the result of squaring the square root. For example, in
 the radicand is 25 and it is the result of squaring the radicand is 25 and it is the result of squaring  , ,
Now let's look at your square root:
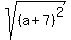
First, since there is no "-" or "+" in front this is a reference to the positive square root. So whatever we end up with for an answer, it must be positive.
Next, this square root represents the number/expression you square to get 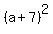 as a result. So what do we square to get as a result. So what do we square to get 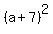 ? The "obvious" answer is: a+7. ? The "obvious" answer is: a+7.
But here is where we can easily go wrong. We can't forget the part about "must be positive". Is a+7 guaranteed to be positive? Since the problem tells us that the variable can be any real number, we must say: No, a+7 is not necessarily positive. So what do we do? Answer: Use absolute value to guarantee a positive square root:

Note: Use the absolute value on the whole expression, not just the variable. 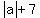 is not correct. is not correct.
|
|
|
| |