|
Question 616452: For which of the following equations is it true that the sum of the roots equals the product of the roots?
A. x^2 - 4 = 0
B. x^2 - 2x +1 = 0
C. x^2 - 4x + 4 = 0
D. x^2 - 5x + 6 = 0
E. x^2 + 4x + 4 = 0
This is a question from a Practice Subject Test I'm taking. The roots of what? How would you compare the sum of the said roots and the product of them? This confuses me.
Thank you very much for any help you can give me!
Found 2 solutions by richwmiller, MathTherapy:
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! x*y=x+y
A) roots are -2 and 2
-2*2=-4
-2+2=0
no
B)1 and 1
1*1 not equal to 2
no
C)x=2 and 2
2*2=2+2
yes
D)3 and 2
3*2 not equal 3+2
no
E)
-2 and -2
no
C) is the only answer
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! For which of the following equations is it true that the sum of the roots equals the product of the roots?
A. x^2 - 4 = 0
B. x^2 - 2x +1 = 0
C. x^2 - 4x + 4 = 0
D. x^2 - 5x + 6 = 0
E. x^2 + 4x + 4 = 0
This is a question from a Practice Subject Test I'm taking. The roots of what? How would you compare the sum of the said roots and the product of them? This confuses me.
Thank you very much for any help you can give me!
A quadratic equation (one of the above) is in the form: 
The sum of the roots (solution for x) is determined by the formula:  , and the product is determined by the formula: , and the product is determined by the formula: 
A. 
For the 1st quadratic,  , a = 1; b = 0; and c = - 4 , a = 1; b = 0; and c = - 4
Therefore, for this quadratic, the sum of the roots becomes: S = 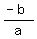 , or S = , or S = 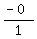 , or 0 , or 0
The product of this quadratic's roots = P =  , or P = , or P = 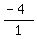 , or - 4 , or - 4
The sum ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ). ).
B. 
For the 2nd quadratic,  , a = 1; b = - 2; and c = 1 , a = 1; b = - 2; and c = 1
Therefore, for this quadratic, the sum of the roots becomes: S = 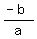 , or S = , or S = 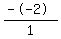 , or 2 , or 2
The product of this quadratic's roots = P =  , or P = , or P = 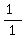 , or 1 , or 1
The sum ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ). ).
C. 
For the 3rd quadratic,  , a = 1; b = - 4; and c = 4 , a = 1; b = - 4; and c = 4
Therefore, for this quadratic, the sum of the roots becomes: S = 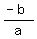 , or S = , or S = 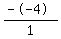 , or 4 , or 4
The product of this quadratic's roots = P =  , or P = , or P = 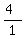 , or 4 , or 4
The sum ( ) of this quadratic's roots is EQUAL to its roots' product ( ) of this quadratic's roots is EQUAL to its roots' product ( ). ).
We have found the quadratic equation that has its roots' sum equal to its roots' product. We do not have to proceed, but I will do so just to make sure there are no others.
D. 
For the 4th quadratic,  , a = 1; b = - 5; and c = 6 , a = 1; b = - 5; and c = 6
Therefore, for this quadratic, the sum of the roots becomes: S = 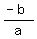 , or S = , or S = 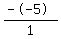 , or 5 , or 5
The product of this quadratic's roots = P =  , or P = , or P =  , or 6 , or 6
The sum ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ). ).
E. 
For the 5th quadratic,  , a = 1; b = 4; and c = 4 , a = 1; b = 4; and c = 4
Therefore, for this quadratic, the sum of the roots becomes: S = 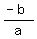 , or S = , or S = 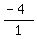 , or - 4 , or - 4
The product of this quadratic's roots = P =  , or P = , or P = 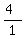 , or 4 , or 4
The sum ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ) of this quadratic's roots is NOT EQUAL to its roots' product ( ). ).
We could've chosen to solve the quadratics and determine their roots, after which we'd add and multiply their individual roots to see if they're equal, but this would've been too time-consuming, so this is an easier method.
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|
| |