SOLUTION: how do you combine the square root of 75a to the third power added to a the square root of 12a

Algebra ->  Square-cubic-other-roots -> SOLUTION: how do you combine the square root of 75a to the third power added to a the square root of 12a      Log On


   

Question 596099: how do you combine the square root of 75a to the third power added to a the square root of 12a
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
I assume by "combine" you mean add:
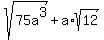
sqrt%2875a%5E3%29+%2B+a%2Asqrt%2812%29
To add square roots (or anything for that matter) they must be alike. Like square roots have the same radicand. ("Radicand" is the name for the expression inside of a radical.) Your radicands are not the same so we cannot add these terms as they are right now.

However, just like you don't leave fractions unreduced, you don't leave square roots unsimplified. Square roots can be simplified if their radicands have factors that are perfect squares. Both of your radicands have perfect square factors. So we can simplify them both.

To simplify a square root
  1. Rewrite the radicand as the product of one (or more) perfect square factors (other than 1) and, possibly, a factor that is not a perfect square.
  2. Use a property of radicals, root%28x%2C+p%2Aq%29+=+root%28x%2C+p%29%2Aroot%28x%2C+q%29, to separate the factors into separate square roots.
  3. Now that the perfect squares are in their own square roots they can be simplified.
Let's see this on your square roots:
1. Factor so that there is at least one perfect square factor. (Remember, not all radicands will have a perfect square factor. These square roots will not simplify.)
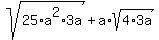
sqrt%2825%2Aa%5E2%2A3a%29+%2B+a%2Asqrt%284%2A3a%29
(Note how I put the perfect square factors in front. This is not required but it makes things easier later on.)

2. Separate the factors:
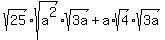
sqrt%2825%29%2Asqrt%28a%5E2%29%2Asqrt%283a%29+%2B+a%2Asqrt%284%29%2Asqrt%283a%29
(Note: Since neither the 3 nor the "a" of 3a is a perfect square, there is no reason to separate them.)

3. Simplify the square roots of the perfect squares:
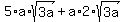
5%2Aa%2Asqrt%283a%29+%2B+a%2A2%2Asqrt%283a%29
or
5%2Aa%2Asqrt%283a%29+%2B+2%2Aa%2Asqrt%283a%29
Since there are no more perfect square factors in either radicand, the square roots are now simplified. (If there were still any perfect square factors in a radicand then repeat the steps above. It's just like reducing a fraction and then realizing that it will reduce some more.)

And look! The terms are now alike. So we can add them now:
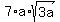
7%2Aa%2Asqrt%283a%29
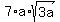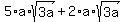(If you have trouble seeing how you get 7%2Aa%2Asqrt%283a%29 from 5%2Aa%2Asqrt%283a%29+%2B+2%2Aa%2Asqrt%283a%29%29, then think of the square root as a variable. Let's say q. So exactly like 5aq + 2aq = 7aq, 5%2Aa%2Asqrt%283a%29+%2B+2%2Aa%2Asqrt%283a%29+=+7%2Aa%2Asqrt%283a%29)