|
Question 411562: Determine the values of the variable for which the expression is defined as a real number.
square root of 16-9x^2
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 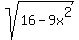
In order for an even-numbered root (square root, 4th root, 6th root, etc.) to be a real nnumber, the radicand (the expression inside the radical) must be non-negative (positive or zero). So in order for your square root to be real, the radicand, 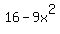 , must be non-negative. In other "words": , must be non-negative. In other "words":

This is a quadratic inequality. These can be solved graphically or algebraically.
Graphical solution to  . .
Consider the equation

If know your equations you will recognize this as a parabola (because of the  but no but no  ) which opens downward (because of the minus in front of the ) which opens downward (because of the minus in front of the  term). The part of this parabola from the x-axis and up (if any) will have y coordinates that are zero or positive. The x values for this part of the parabola represent the solution to your problem because term). The part of this parabola from the x-axis and up (if any) will have y coordinates that are zero or positive. The x values for this part of the parabola represent the solution to your problem because- those x's make y zero or positive
- Since
 , those same x's will make , those same x's will make 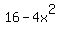 zero or positive. zero or positive. - We are looking for the x's that make
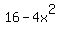 zero or positive. zero or positive.
Here's a graph to help you see this:
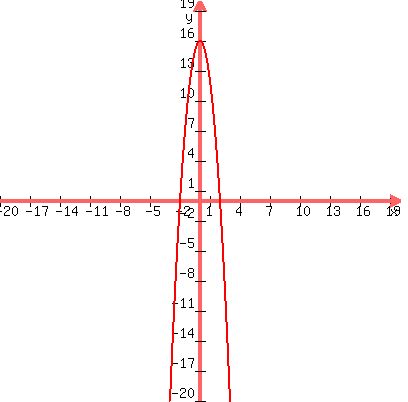
We are looking for the x's in that "bump" from the x-axis and up. The x's that make 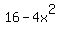 zero will be where the "bump" intersects the x-axis. We want these x values and everything in between. zero will be where the "bump" intersects the x-axis. We want these x values and everything in between.
To find the x-intercepts we set y to zero (because y is zero on the x-axis) and solve the equation:

Factoring we get:
(4+3x)(4-3x) = 0
From the Zero Product Property we know that one of these factors must be zero:
4+3x = 0 or 4-3x=0
Solving these we get:
x = -4/3 or x = 4/3
So the solution to your problem is all x's between -4/3 and 4/3, inclusive. In algebraic notation this is:

An algebraic solution for 
First we factor:
(4+3x)(4-3x) >= 0
We have a product that is greater than or equal to zero. With a little thought we can figure out there are two ways this could happen:- Both factors are positive (or zero)
- Both factors are negative (or zero)
Algebraically "both factors are positive (or zero)" is expressed as:
 and and 
Algebraically "both factors are negative (or zero)" is expressed as:
 and and 
And finally to "say" that one or the other of these is true would be:
( and and  ) or ( ) or ( and and  ) )
We can solve this compound inequality. Solving each of the individual inequalities we get:
( and and  ) or ( ) or ( and and  ) )
(Note: If you cannot see how the 2nd and 4th inequalities work out the way they do, see below.)
The first pair can be expressed as  which is the same answer we got in the graphical solution. The second pair has NO solution because it is impossible for x to be less than or equal to -4/3 and greater than or equal to 4/3 at the same time! which is the same answer we got in the graphical solution. The second pair has NO solution because it is impossible for x to be less than or equal to -4/3 and greater than or equal to 4/3 at the same time!
So either graphically or algebraically the solution is:

If you had trouble solving the 4-3x inequalities....
Because of the minus in front of the x these are a little tricky to solve. For example:

Most people would start by subtracting 4 from each side:

and then dividing by -3. But here is the "trick". We have to remember the special rule that applies whenever you multiply or divide both sides of an inequality by any negative number: You must reverse the inequality symbol! So when we divide by -3 the inequality gets reversed:

|
|
|
| |