SOLUTION: How would you evaluate an expression with a mixed-number exponent such as 8^1 1/3?

Algebra ->  Square-cubic-other-roots -> SOLUTION: How would you evaluate an expression with a mixed-number exponent such as 8^1 1/3?       Log On


   

Question 374185: How would you evaluate an expression with a mixed-number exponent such as 8^1 1/3?
Found 2 solutions by Fombitz, jsmallt9:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
DUPLICATE See Square-cubic-other-roots/374194:

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!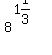
8%5E%281%261%2F3%29
Mixed numbers are almost always a pain. I usually recommend that they be converted to improper fractions. It is the same here. So we will start by changing 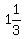1%261%2F3 to 4/3:
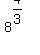
8%5E%284%2F3%29
If you are still not sure how to simplify this, I recommend writing the exponent in a factored form. In this case, we would rewrite the expression as:
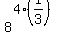
8%5E%284%2A%281%2F3%29%29
Since
8%5E%284%2A%281%2F3%29%29+=+%288%5E4%29%5E%281%2F3%29
which says that we raise 8 to the 4th power and then, because an exponent of 1/3 means cube root, find the cube root of the answer.
Also, since multiplication is Commutative, we are free to change the order:
8%5E%28%281%2F3%29%2A4%29+=+%288%5E%281%2F3%29%29%5E4
which says to find a cube root and then raise to the 4th power.

So, in summary, an exponent of 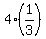4%2A%281%2F3%29 means we will raise to the 4th power and we will find a cube root and we get to choose the order in which these are done!

Since 8 is a perfect cube (8+=+2%5E3), it seems to me that finding the cube root first will be easier than raising 8 to the 4th power. So here's the problem from start to finish:


(Note: even if you decide to raise to the 4th power first and then find the cube root, you still end up with 16.)