SOLUTION: Why does √xy = √x√y?

To prove 

Let x and y be non-negative real numbers. 

lemma: square roots of non-negative real numbers are unique.

Proof:
For contradiction, suppose for positive real number " a ", p and q 
are two different non-negative square roots of " a ".  Then,

 =>  =>  
since , p-q=0, so p=q.  So we have reached a contradiction 
namely, that p and q are NOT different.

We show that the squares of 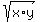 and 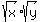 are equal.





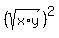
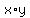
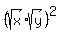
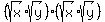
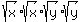
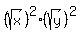
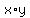Therefore 

and by the lemma, 

PROVED.

Edwin