Suppose a = -2
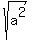

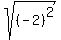




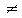
 Not equal!
But
Not equal!
But 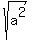


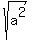

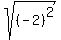





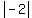

 Equal!
The definition of absolute value is
Equal!
The definition of absolute value is 

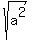 When the radical
When the radical 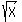 is used, it is always either positive
(or zero, in the case
is used, it is always either positive
(or zero, in the case 

 ), but
), but 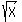 is never negative!
Although we often say "SQUARE ROOT OF X" when we see
is never negative!
Although we often say "SQUARE ROOT OF X" when we see 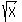 , we
really should say "NON-NEGATIVE SQUARE ROOT OF X".
[It's like in geometry, we often say "line" when we really should say
"line segment".]
Edwin
, we
really should say "NON-NEGATIVE SQUARE ROOT OF X".
[It's like in geometry, we often say "line" when we really should say
"line segment".]
Edwin