SOLUTION: Determine the values of the variable for which the expression is defined as a real number. fourth root of(1-x)/(2-x)

Algebra ->  Square-cubic-other-roots -> SOLUTION: Determine the values of the variable for which the expression is defined as a real number. fourth root of(1-x)/(2-x)      Log On


   

Question 1100913: Determine the values of the variable for which the expression is defined as a real number.
fourth root of(1-x)/(2-x)
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
In a normal mathematical language, this post must sound in this way: 
   
    Find the domain of the function  fourth root of (1-x)/(2-x).

Solution 

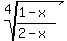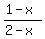f(x) = root%284%2C%281-x%29%2F%282-x%29%29.      (1)

The domain is the set of those real numbers, where the expression under the root is non-negative:

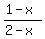    %281-x%29%2F%282-x%29 >= 0.      (2)

So, we need to find the solution set of this inequality.


The rational function (2) has two critical points: x= 1  and  x= 2  (in ascending order).

1)  If x <= 1, then both binomial are non-positive:  

              1-x <= 0  and  2-x < 0.

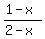              Hence, the ratio  %281-x%29%2F%282-x%29 is non-negative in this domain 

              and the set  x <= 1  DOES BELONG  to the set of solutions to inequality (2).



2)  If 1 < x <2, then the binomial 1-x is positive  and  the binomial 2-x is negative:

              1-x > 0   and  2-x < 0.

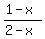              Hence, the ratio  %281-x%29%2F%282-x%29 is negative in this domain 

              and the set  1 < x < 2  DOES NOT BELONG  to the set of solutions to equation (2).



2)  If x > 2, then both binomials  1-x  and  2-x  are greater than 0:  

              1-x > 0  and  2-x > 0.

              Hence, the ratio  %281-x%29%2F%282-x%29 is positive in this domain 

              and the set  x > 1  DOES BELONG  to the set of solutions of inequality (2).

Answer. The domain of the given function is the set (-infinity,1] U (2,infinity).


Solved.


----------------
To see more examples of solved problems on inequalities and finding function domains, look into these relevant lessons
    - Solving problems on quadratic inequalities,
    - Solving inequalities for high degree polynomials factored into a product of linear binomials
    - Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
    - Solving inequalities for rational functions with non-zero right side
    - Advanced lesson on inequalities

    - Domain of a function which involves a quadratic polynomial under the square root operator,
    - Domain of a function containing high degree polynomial under the square root operator
    - Domain of a function which is the square root of a rational function
in this site.


Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic  "Inequalities".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.