|
Question 1094824: Solve the equation x^3-9x+10=0 , expressing non-integer roots in the form c+/-d(sqrt6) , where c and d are integers.
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
x^3-9x+10 = 0 .
1. Notice that x= 2 is the root.
2. According to the Remainder theorem, it means that the given polynomial of degree 3 is divided by the binomial (x+2) without a remainder.
3. Divide x^3-9x+10 by (x+2) (long division).
You will get a quadratic polynomial.
4. Find the roots of this quadratic polynomial using quadratic formula.
That's all.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Solve the equation x^3-9x+10=0 , expressing non-integer roots in the form c+/-d(sqrt6) , where c and d are integers.
You can start here ====> 2 is an INTEGER root, so x = 2, and x - 2 = 0, so a factor is: x - 2.
You then divide 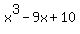 by x - 2 to get a QUADRATIC trinomial.
Using this trinomial and the quadratic equation formula, you'll be able to get the other 2 roots.
Finally, present the other 2 roots in the requested form.
|
|
|
| |
