|
Question 1094775: A rectangular block has a square base. The length of each side of the base is (√3 - √2)m and volume of the block is (4√2 - 3√3) cubic metre. Find the height of the block in the form (a√2 + b√3) where a and b are constants.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE WORD PROBLEM PART:
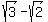 = length of a side of the square base in meters. = length of a side of the square base in meters.
 = surface area of the square base in square meters. = surface area of the square base in square meters.
With that and the 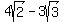 volume of the block in cubic meters, volume of the block in cubic meters,
knowing that volume = (area of the base)(height),
we can calculate the height in meters as
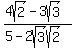 or or 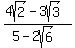 . .
HOW TO SIMPLIFY THAT QUOTIENT:
To get rid of the irrationality in the denominator,
you need to do something you probably do almost often: rationalize.
In math, you do that by multiplying numerator and denominator times the irrational number that will result in a rational denominator.
In thid case, the irrational factor we need to multiply by is 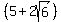 , ,
because  . .
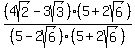 or or 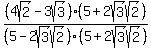
With either of those equivalent expressions, the denominator is  , ,
and all you have to do is carefully calculate the numerator,
without making mistakes.
You could calculate it as
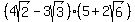    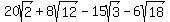  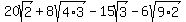  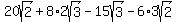  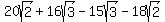   . .
Or you could calculate it as
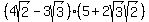 
 
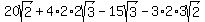 
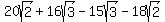 
 . .
VERIFYING YOUR ANSWER:
You could also calculate approximate values for
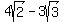    and and
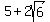   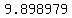 , ,
and then multiply them together to find the height in meters as
 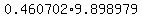   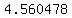 . .
That is not the answer "in the form of 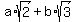 ," ,"
but it is easy to calculate with a computer or calculator,
and a way to verify if you made a mistake.
Another way to verify the answer
is to multiply area in square meters = times the answer you found:
 

 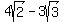 . .
NOTE: I have not yet decided if assigning this problem is a way to give students practice with square roots, or a way to torture them. I suppose that assigning one or two such exercises would drive home
1. the need to understand the situation in word problems to figure out the needed calculations ,
2. the idea of "rationalizing" denominators by multiplying "conjugate irrational numbers" as a pair of irrational numbers like 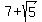 and and  , and , and
3. the idea of simplifying roots as in  . .
|
|
|
| |