Questions on Algebra: Square root, cubic root, N-th root answered by real tutors!

Tutors Answer Your Questions about Square-cubic-other-roots (FREE)

Question 99970: Please help. I have one last problem on my test due tonight. I know I am not giving you a lot of time but the person that usually helps me has ended up in the hospital and I am stuck on this last question.
Solve sqrt2x-1=sqrt4x-1 with another -1 outside the sqrt part.
Thanks if you have the time.
Click here to see answer by MathTherapy(10702)

Question 648428: please help me solve this equation:
sqrt ( 32 ) times(multiply) sqrt ( 6 )

i am trying to simplify this equation down to a number and a square root..
my last step i got
sqrt ( 8 ) (times) sqrt ( 4 ) (times) sqrt ( 6 )
and i dont know what to do next...
thank you in advance for your help!

Click here to see answer by MathTherapy(10702)

Question 51682: I have the answer in the back of the book. Still having trouble getting there.
4^2/3 * 6^2/3 * 9^2/3
Have tried squaring 4 and then taking the cubed root but don't get good numbers.
The book says answer is 36?????
Click here to see answer by MathTherapy(10702)

Question 252005: Can you please help me with this equation: 2- sqrt 7 / sqrt 3 - sqrt 2
the answer I have is (2- sqrt 7)(sqrt 3 + sqrt 2 / 5 but i don't think it is right.
Click here to see answer by MathTherapy(10702)

Question 96313: 3 * 2
Click here to see answer by greenestamps(13292)

Question 96313: 3 * 2
Click here to see answer by MathTherapy(10702)

Question 1164689: c) The equation of a curve is y = squrt of 5x + y
i. Calculate the gradient of the curve at the point where x = 1
ii. A point with coordinates (x,y) moves along the curve in such a way that
the rate of increase of x has the constant value 0.03 units per second. Find
the rate of increase of y ath the instant when x = 1.
iii. Find the area enclosed by the curve, the x - axis, the y - axis and the line
y = 1.
Click here to see answer by ikleyn(53570)

Question 485853: What is 9 divided by the cubed root of 3?
Click here to see answer by MathTherapy(10702)

Question 308197: What is the cubed root of 4x squared divided by the cubed root of 16?
Click here to see answer by MathTherapy(10702)

Question 457475: How do I solve and algebra problem with a squared variable? 25=16-Tsquared

Click here to see answer by ikleyn(53570)

Question 262842: Simplify:
(sqrt(50) - 2sqrt(5))(5sqrt(2) + sqrt(20))
Click here to see answer by MathTherapy(10702)

Question 983405: Cuberoot of 32.768 with steps.
Click here to see answer by MathTherapy(10702)

Question 236908: I am reveiwing algebra on my own in my old age. I am stumped on a problem. I need to find the 6th root of 225. I have broken the equation down into the square and the 3rd root, but cannot find the book answer which is the cube root of 15. Can you help? I am over half way through the book and do not move on until I have solved all of the odd numbered problems and checked my answers against the book answers.
Click here to see answer by MathTherapy(10702)

Question 100682: Good Evening Tutor,
I have two questions I was wondering if you could tell me if I got them correct?
1.) Evaluate if possible: cubed(3) sqrt of -8/27 I got - 1/6 is this correct?
2.) simplify by combining like terms. sqrt of 63 - 2 sqrt of 28 + 5 sqrt of 7.
I got 7 sqrt of 7 I think this is wrong but I am not sure where I am getting messed up I keep getting the same answer.
Any help is appreciated. Thank you.
Click here to see answer by MathTherapy(10702)

Question 1117168: solve Sqrt {2+sqrt {3}}
Click here to see answer by MathTherapy(10702)

Question 717026: one number is twice the another number and their product is 2048 . what are the two number
Click here to see answer by ikleyn(53570)

Question 202363: if (125/27)^x = the cubic root of 0.6 then the value of x is _______

Click here to see answer by greenestamps(13292)

Question 202363: if (125/27)^x = the cubic root of 0.6 then the value of x is _______

Click here to see answer by ikleyn(53570)

Question 243853: cube root of 27w to the 12th power over 100

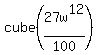
Explanation:
I am a volunteer math tutor. My student disagrees with the answer I came up with, so I am writing to you for any help in justifying her answer or my answer as "more correct". Here's the problem: Show your work in solving this cube root problem.
The heart of the question is my student's answer vs. my answer. Which one is more correct?
Student:
cube( (3 x 3 x 3) w^(4 x 3)/(75 + 25) )
3w4/(5 x 5 x 5) + cube( 25 )
3w4/5 + cube ( 25 ) <<< student's answer
Tutor:
cube( (3 x 3 x 3) w^(4 x 3)/(75 + 17 + 8) )
3w4/(5 x 5 x 5) + cube( 17 ) + (2 x 2 x 2)
3w4/5 + cube ( 17 ) + 2
3w4/7 + cube (17) <<< tutor's answer
Which answer will the teacher of my student consider as "correct" ?
3w4/5 + cube ( 25 ) OR 3w4/7 + cube (17)
Thank you. Rob Miller
Click here to see answer by MathTherapy(10702)

Question 558894: use the square root property to solve the equation

(1) (x+1)^2=9

(2) x^2=121

Click here to see answer by ikleyn(53570)

Question 1181912: Al-khwarizmi solved all quadratic equations by reducing them to one of six standard forms, which were then easily solvable. He described the standard forms in terms of “squares”,”roots”, and “numbers”. Here are al-khwarizmis six standard forms.
1. Squares equal to roots(example:ax^2=bx)
2. Squares equal to numbers(example:ax^2=c)
3.roots equal to numbers(example:bx=c)
4.squares and roots equal to numbers (example:ax^2+bx=c)
5. Squares and numbers equal to roots (example: ax^2+c=bx)
6.roots and numbers equal to tot squares(example:ax^2=bx+c)
Which method would you use to solve each of the six forms? Why would you use that method?
Write a quadratic equation that can be reduced to one of al-khwarizmis six forms.
Click here to see answer by CPhill(2189)

Question 1209713: Let a and b be integer such that (2 + sqrt(5))(137) = a + b sqrt(5). Compute a^2 - 5b^2.
Click here to see answer by greenestamps(13292)

Question 1183944: Al-Khwarizmi solved all quadratic equations by reducing them to one of six standard forms, which were then easily solvable. He described the standard forms in terms of "squares," "roots," and "numbers." Here are al-Khwarizmi's six standard forms:
squares equal to roots (Example: ax2= bx
a x squared equals space b x)
squares equal to numbers (Example: ax2= c
a x squared equals space c)
roots equal to numbers (Example: bx=c
b x equals c)
squares and roots equal to numbers (Example: ax2+bx=c
a x squared plus b x equals c)
squares and numbers equal to roots (Example: ax2+c=bx
a x squared plus c equals b x)
roots and numbers equal tot squares (Example: ax2=bx+c
a x squared equals b x plus c)
Activity Instructions
• Which method would you use to solve each of the six forms? Why would you use that method?
• Write a quadratic equation that can be reduced to one of al-Khwarizmi's six forms.
Click here to see answer by CPhill(2189)

Question 1209707: Let (2 + \sqrt{5})(137) = a + b \sqrt{5}, where a and b are integers. Compute a^2 - 5b^2.

Click here to see answer by CPhill(2189)

Question 1209597: Find all values of x satisfying
sqrt(4x - 3) + 40/sqrt(4x - 3) = 12x + 14.
Click here to see answer by ikleyn(53570)

Question 1209551: I have to solve an square root without a calculator. It has to be in a(square root symbol) b. Help please!
Click here to see answer by ikleyn(53570)

Question 1209551: I have to solve an square root without a calculator. It has to be in a(square root symbol) b. Help please!
Click here to see answer by mccravyedwin(419)

Question 1209551: I have to solve an square root without a calculator. It has to be in a(square root symbol) b. Help please!
Click here to see answer by Edwin McCravy(20077)

Question 1209551: I have to solve an square root without a calculator. It has to be in a(square root symbol) b. Help please!
Click here to see answer by math_tutor2020(3831)

Question 1209102: Arrange the following numbers in increasing order (smallest first, biggest last):
A = 2^(1/2)*4^(1/6)*8^(1/3)
B = 12*128
C = 8^(1/5)^2*8^(1/5)^3
D = 4*(-1)*2*(-1)*8*(-1)
E = 2^(1/2)*3*4^(1/4)
Click here to see answer by MathTherapy(10702)

Question 1209119: The difference of two positive numbers is 99. The numbers multiply to 630. What is the sum of their squares?
Click here to see answer by ikleyn(53570)

Question 1209119: The difference of two positive numbers is 99. The numbers multiply to 630. What is the sum of their squares?
Click here to see answer by math_tutor2020(3831)

Question 1209035: What is the smallest positive integer n such that \sqrt[4]{675 + n} is an integer?
Click here to see answer by greenestamps(13292)

Question 1208754: Find the range of y = sqrtx - 2}.

Click here to see answer by greenestamps(13292)

Question 1208359: Simplify sqrt{4x^3•9y^5}.

Click here to see answer by ikleyn(53570)

Question 1208359: Simplify sqrt{4x^3•9y^5}.

Click here to see answer by mccravyedwin(419)

Question 1208359: Simplify sqrt{4x^3•9y^5}.

Click here to see answer by math_tutor2020(3831)

Question 1208359: Simplify sqrt{4x^3•9y^5}.

Click here to see answer by josgarithmetic(39720)

Question 1208358: Why does √xy = √x√y?

Click here to see answer by mccravyedwin(419)

Question 1208360: Simplify cube root{27x^3•y^3•z^5}.

Click here to see answer by josgarithmetic(39720)

Question 1207378: Give an example to show that sqrt{a^2} is not equal to a. Use it to explain why sqrt{a^2} = |a|.
Click here to see answer by mccravyedwin(419)

Question 1207360: Rationalize the denominator.

Let cr = cube root.

5/(cr(2))

Let me see.

5/(cr(2)) • (cr(2))/(cr(2))

5(cr(2))/(2)
The book's answer is different.

P. S. How do I upload math photos (geometric figures, graphs of functions, etc) on this site?

Click here to see answer by MathTherapy(10702)

Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380