Question 934020: Algebra Find the unknown digit to make each statement ture
2.48 > 2.4n1 > 2.463 What goes in digit n and how do we determine this?
5.723 < 5.72n < 5.725
7.64 < 7.n5 < 7.68
Answer by Techpriest(29)   (Show Source): (Show Source):
You can put this solution on YOUR website! 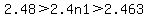
By using trial and error. By looking at the hundredth digit, we know that the first number of the hundred digit is 8 and the hundredth digit of the third number is 6. We have to find a value less than 8, but greater than 6. Therefore, we can assume that n is 7. Now, we plug in our values.
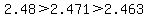
Plugging in our values, this statement is true and n can be 7.
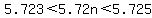
By also using trial and error, we look this time the thousandth digit, we know that the first number of the digit is 3 and the third number of the digit is 5. We need to find a value greater than 3, but less than 5. A value that is greater than 3, but less than 5 would be 4. Plugging in 4 would be...

Correct.
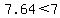
Using the same method, we look at the tenth digit now, we know that the first number of the tenth digit is 6 and the third number of the digit is also 6. Since the first and third number of the tenth digit are the same, we look to the hundredth digit that the first number is 4 and the third number is 8. Relevant to the solution, the second number of the hundredth digit is 5. We want to find a value for n that makes the second number greater than 7.64, but less than 7.68. Through trial and error as usual, we discover that n must equal 6.
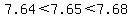
Plugging in the value of n. This statement now appears to be true.
|
|
|