Question 1208990: A 5-horsepower (hp) pump can empty a pool in 5 hours.A smaller, 2-hp pump
empties the same pool in 8 hours. The pumps are used together to begin emptying
this pool.After two hours, the 2-hp pump breaks down. How long will it take the
larger pump to empty the pool?
Let hp = horsepower
5hp = 1/5
2hp = 1/8
Let t = time in hours
1/t = time it takes larger pump to empty the pool
My equation is:
(1/5) + (1/8) = 1/t
Is this correct?
Found 4 solutions by ikleyn, MathTherapy, AnlytcPhil, greenestamps:
Answer by ikleyn(53451)   (Show Source): (Show Source):
Answer by MathTherapy(10602)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A 5-horsepower (hp) pump can empty a pool in 5 hours.A smaller, 2-hp pump empties the same pool in 8 hours. The pumps are used together to begin emptying this pool.After two hours, the 2-hp pump breaks down. How long will it take the larger pump to empty the pool?
Let hp = horsepower
5hp = 1/5
2hp = 1/8
Let t = time in hours
1/t = time it takes larger pump to empty the pool
My equation is:
(1/5) + (1/8) = 1/t
Is this correct?
No. That's WRONG.
Yes, the rates are 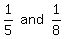 . However, both worked TOGETHER, for 2 hours, so fraction of job completed in 2 hours = . However, both worked TOGETHER, for 2 hours, so fraction of job completed in 2 hours = 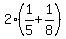 And, since the SLOWER pump broke down and the FASTER completed the job, the FASTER completed the remaining fraction:
And, since the SLOWER pump broke down and the FASTER completed the job, the FASTER completed the remaining fraction:
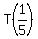 , with T being the time taken by the FASTER to complete the job.
Both fractions SUM to 1, so equation is actually: , with T being the time taken by the FASTER to complete the job.
Both fractions SUM to 1, so equation is actually:  Solve that now for T, the time it takes the LARGER/FASTER to complete the job.
Solve that now for T, the time it takes the LARGER/FASTER to complete the job.
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A 5-horsepower (hp) pump can empty a pool in 5 hours.
So the larger pump's emptying rate is 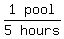 or or 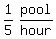 A smaller, 2-hp pump empties the same pool in 8 hours.
So the smaller pump's emptying rate is
A smaller, 2-hp pump empties the same pool in 8 hours.
So the smaller pump's emptying rate is 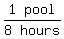 or or 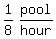 The pumps are used together to begin emptying this pool.
Their rates add together so their combined rate is
The pumps are used together to begin emptying this pool.
Their rates add together so their combined rate is
  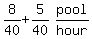  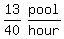 After two hours,... [the 2-hp pump breaks down.]
So RATE x TIME = FRACTION of the pool EMPTIED
After two hours,... [the 2-hp pump breaks down.]
So RATE x TIME = FRACTION of the pool EMPTIED
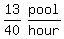    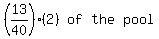  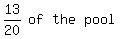 Since 13/20ths of the pool has been emptied, there remain 7/20th of the pool
to be emptied
How long will it take the larger pump to empty the pool?
Now the TIME is an unknown, so we use a letter, say t:
Again, RATE x TIME = FRACTION of the pool EMPTIED, but now, we use only the rate
of the larger pump, 1/5, and only the remaining 7/20 of the pool to be emptied.
Since 13/20ths of the pool has been emptied, there remain 7/20th of the pool
to be emptied
How long will it take the larger pump to empty the pool?
Now the TIME is an unknown, so we use a letter, say t:
Again, RATE x TIME = FRACTION of the pool EMPTIED, but now, we use only the rate
of the larger pump, 1/5, and only the remaining 7/20 of the pool to be emptied.
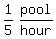  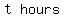  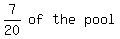 So the equation is
So the equation is
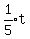   Multiply both sides by 20
Multiply both sides by 20
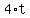  
  
  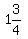 hours
1 hour and 45 minutes.
Edwin hours
1 hour and 45 minutes.
Edwin
Answer by greenestamps(13258)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A 5-horsepower (hp) pump can empty a pool in 5 hours. A smaller, 2-hp pump empties the same pool in 8 hours. The pumps are used together to begin emptying this pool. After two hours, the 2-hp pump breaks down. How long will it take the larger pump to empty the pool?
The question that is asked is almost certainly not the intended question: "How long will it take the larger pump to empty the pool?". The given information tells us the answer -- it takes 5 hours for the larger pump to empty the pool.
The question that should be asked is "How long will it take the larger pump to FINISH EMPTYING the pool?"
As in several other questions you have posted to which I have posted responses, my primary message to you is to take the time to write out clear definitions of the variables and expressions you are using, so that it is easier to form the correct equation(s) for solving the problem.
Let's look at the work you show and see how to make it better -- so that you are more likely to be able to solve the problem correctly.
Let hp = horsepower
That is unnecessary and potentially confusing. When solving a problem using formal algebra, "let..." is used to define a variable or expression you are going to use in solving the problem. The horsepowers of the two pumps are of no concern in the problem.
5hp = 1/5
2hp = 1/8
YOU know what you mean there, but it doesn't help you set up the problem correctly, because its meaning is not clear.
"1/5" and "1/8" are important expressions for solving the problem, but you want to take the time to write out definitions of EXACTLY what those espressions represent.
Given that the larger pump alone can empty the pool in 5 hours and the smaller pump alone can empty it in 8 hours, what you should say here is something like this:
1/5 = fraction of pool emptied by the larger pump in 1 hour
1/8 = fraction of pool emptied by the smaller pump in 1 hour
Let t = time in hours
Time for what? The two pumps work for different numbers of hours....
1/t = time it takes larger pump to empty the pool
1/t is not an amount of time; t is an amount of time. If t were the number of hours it takes to do a job, then 1/t would be the fraction of the job done in 1 hour. But in your setup it's not clear what "t" is, because the two pumps work for different numbers of hours.
My equation is:
(1/5) + (1/8) = 1/t
Again we don't know here what "t" is.
This would be the equation (undoubtedly in the form used in the reference you are using) if the two pumps were both working for "t" hours. But they are working for different numbers of hours.
For correct formal algebraic solutions to the problem (which you probably need), look at any of the responses you have already received.
However, for an informal solution, I would do something like the following.
The smaller pump can empty the pool alone in 8 hours, so it can empty 1/8 of the pool in 1 hour. It works for 2 hours before breaking down, so the fraction of the pool it empties is 2/8 = 1/4.
So the larger pump empties the remaining fraction of the pool, which is 3/4. It can empty the pool alone in 5 hours, so to empty 3/4 of the pool it requires 3/4 of 5 hours, which is (3/4)*5 = 15/4 = 3 3/4 hours. When the smaller pump breaks down, it has already worked for 2 hours, so the number of hours it needs to work alone to finish the job is 3 3/4 - 2 = 1 3/4 hours.
ANSWER: 1 3/4 hours
|
|
|