Question 1208035: Find the domain, range, and intercepts of the function
A(x) = 4x•sqrt{1 - x^2}. Finally, graph the function.
Found 5 solutions by Edwin McCravy, math_tutor2020, mccravyedwin, ikleyn, AnlytcPhil:
Answer by Edwin McCravy(20077)   (Show Source): (Show Source):
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
Answer by mccravyedwin(418)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 We find the x-intercept(s) by setting A(x) = 0
We find the x-intercept(s) by setting A(x) = 0

 ; ; 
 ; ; 

 So the x-intercepts are (-1,0), (0,0), (1,0
We find the y-intercept(s) by setting x = 0
So the x-intercepts are (-1,0), (0,0), (1,0
We find the y-intercept(s) by setting x = 0

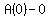 So the y-intercept is (0,0) which is both an x- and a y-intercept.
So the y-intercept is (0,0) which is both an x- and a y-intercept.
 Since a square root's radicand cannot be negative
Since a square root's radicand cannot be negative

 So either both factor are positive or both negative
So either both factor are positive or both negative
 OR OR 
 OR OR  So the domain is
So the domain is  or in interval notation [-1,1] or in interval notation [-1,1]
 For the range, we must find the maxima and minima
For the range, we must find the maxima and minima





 We can factor the -1/2 power out of both terms and since
We can factor the -1/2 power out of both terms and since  ,
we will just have the 1st power of the parenthetical expression: ,
we will just have the 1st power of the parenthetical expression:
 Now I'll let you simplify that down to
Now I'll let you simplify that down to
 Set that = 0 and you get the x-coordinates of the maximum and minimum points
Set that = 0 and you get the x-coordinates of the maximum and minimum points




 Substituting:
Substituting:
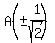 = = 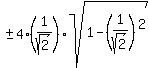
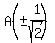 = = 
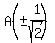 = = 
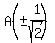 = = 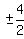
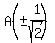 = = 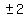 So the range is
So the range is  or in interval notation [-2,2]
Edwin or in interval notation [-2,2]
Edwin
Answer by ikleyn(53451)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the domain, range, and intercepts of the function
A(x) = 4x•sqrt{1 - x^2}. Finally, graph the function.
~~~~~~~~~~~~~~~~~~~
In this problem, finding domain is a simple elementary task: the domain is [-1,1].
Finding x-intercepts is also simple elementary task: they are -1, 0 and 1 on x-axis.
The key issue is to find the range.
Tutor Edwin made it in his post, using derivatives and Calculus; it requires a painstaking technique.
Here I will show another way to find the range, which uses simple elementary Algebra with minimum calculations.
Let real number "t" belongs to the range. It means that
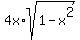 = t (1)
for some value of x. Square bot sides of (1). You will get = t (1)
for some value of x. Square bot sides of (1). You will get
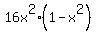 = t^2 = t^2
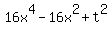 = 0. (2)
You can consider equation (2) as a quadratic equation relative = 0. (2)
You can consider equation (2) as a quadratic equation relative  .
The condition that it has a real solution for .
The condition that it has a real solution for  is this inequality for the discriminant is this inequality for the discriminant
 >= 0, or >= 0, or 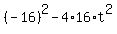 >= 0, or 256 >= >= 0, or 256 >= 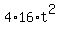 .
It implies .
It implies  <= 4; hence, |t| <= 2, or -2 <= t <= 2.
Thus, equation (1) has a real solution if and only if -2 <= t <= 2.
So, the range of the function <= 4; hence, |t| <= 2, or -2 <= t <= 2.
Thus, equation (1) has a real solution if and only if -2 <= t <= 2.
So, the range of the function 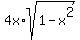 is this interval -2 <= t <= 2, or t belongs [-2,2]. ANSWER is this interval -2 <= t <= 2, or t belongs [-2,2]. ANSWER
Solved.
Thus, this problem can be solved in this simple way much easier than applying Calculus.
Surely, the Calculus approach is like a heavy army tank: it is universal and works everywhere.
So, if you know Calculus and do not afraid to apply it, boldly go forward.
But if the teacher gave you similar problem long before you learn Calculus,
know and remember that this method from my post probably works.
This problem is a typical Math Olympiad level problem or a Math circle level problem
for 9-th grades high school students, who just know Algebra, but still don't know Calculus.
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The student said in a thank-you note to me:
"This is probably your best reply ever."
So I assume s/he is a calculus student. It seemed likely to me because
teachers do not assign Math Olympiad type problems to students. But finding
the range makes this a very good maxima and minima problem. Only a calculus
teacher would assign this. It requires the factoring of a -1/2 power out of
a 1/2 power, leaving a power of 1, which is a necessary technique in
taking derivatives of expressions involving roots. That's because the
product and quotient rules for differentiation often involve exponents which
differ by one, whenever the power rule is used, which is always the case in
expressions with roots.
Edwin
|
|
|